Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 86
Caso seja tangente a alguma hipérbole de focos e , obtenha uma equação de .
Passo 1
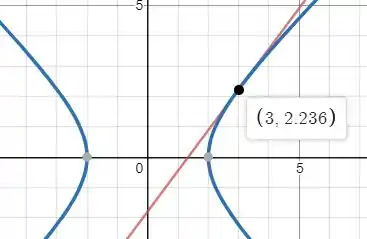
Plotando a reta e os dois pontos dos focos da letra a vemos que a reta corta a reta que liga os dois pontos, então há uma hipérbole que é tangente. E se adotarmos o ponto de tangência como , então se aplicarmos esse ponto na equação da reta tangente vemos que:
E se a equação da hipérbole for algo da forma
Então a equação da reta tangente será algo como:
Reescrevendo a equação tangente dada teremos:
Então:
Primeiro teste seria dizer que e , com isso vemos que os valores de e satisfazem a equação da reta tangente, então a equação dessa hipérbole, será:
Passo 2
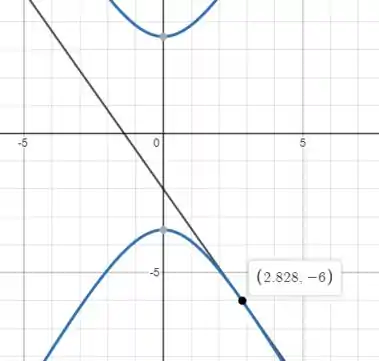
Plotando os dois pontos de foco e a equação de tangente da letra vemos que existe sim uma hipérbole que tangencia essa reta.
Mesma história, dizendo que é o ponto de tangência então:
E a equação de tangente estará sob forma de:
Arrumando a equação de teremos:
Dessa forma:
E se fizermos , e e vemos que o par não bate com a equação da reta tangente.
Portanto:
Por conta do foco, então:
E:
Isso nos dá um sistema igual a:
Aplicando o segundo no primeiro nós teremos:
Portanto , e com isso:
Agora vem uma de sinal, com esses valores poderíamos encontrar dois valores de e , tais como:
O único par que bate com a equação da reta tangente será:
Portanto na hipérbole a parte em é negativa, nos dando uma equação igual a:
Passo 3
Plotando a equação da reta e os dois pontos de foco da letra c vemos que a reta não separa os dois focos
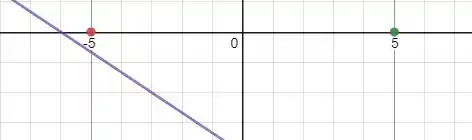
Então não há equação de tangente para uma hipérbole com esses focos. Uma solução é ver onde essa reta está quando .