Chama-se baricentro de um triângulo ao ponto de interseção de suas três medianas. Determine as coordenadas do baricentro do triângulo ABC nos seguintes casos:

Faaaala, galera!

Como o enunciado já diz, o baricentro é a interseção das três medianas de um triângulo. Primeiramente, devemos entender de maneira visual o que isso significa. Observe a imagem abaixo. Ela representa a definição do baricentro, em que são traçadas as retas , e que são as medianas de cada seguimento do triângulo e o ponto de interseção é o baricentro.

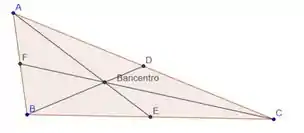
Sabendo dessas informações podemos calcular as coordenadas. Para calcular a coordenada do baricentro, devemos somar as três abscissas dos pontos e dividir por três. Logo, temos:

Para calcular a coordenada y, devemos realizar o mesmo cálculo, porém considerando a soma das ordenadas. Logo, temos:

Logo, as coordenadas do baricentro deste triângulo serão:

Tranquilo?