Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 5.Problemas - Ex. 8
Prove que o segmento de reta que une os pontos médios das laterais de um trapézio é paralelo às bases e sua medida é a média aritmética das medidas das bases.
Passo 1
Faaaala, galera! Tudo certo?
Observe a figura a seguir.
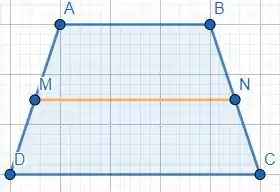
Considere o trapézio , em que é a base menor e é a base maior, são duas bases paralelas. Temos que o seguimento é a base média, em que é o ponto médio de e é o de . Temos então:
Logo, temos que:
Prontinho! Questão finalizada!
Resposta
Demonstração no Passo 1.
Exercícios de Livros Relacionados
Dado o vetor v → = ( 2 , - 1 , - 3 ) , determinar o vetor paralelo a v → que tenhac) sentido contrário ao de v → e módulo 5
Dado o vetor v → = ( 2 , - 1 , - 3 ) , determinar o vetor paralelo a v → que tenhab) o mesmo sentido de v → e módulo 4
Determinar o valor de y para que seja equilátero o triangulo de vértices A(4,y,4), B(10,y,-2) e C(2,0,-4)
Obter um ponto P do eixo das abscissas equidistante dos pontos A(3,-1,4) e B(1,-2,-3)
Obter um ponto P do eixo das cotas cuja distância ao ponto A(-1,2,-2) seja igual a 3