Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.8 - Ex. 9
Quais condições devem ser satisfeitas por e para que o sistema linear sobredeterminado.
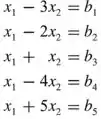
Seja consistente?
Passo 1
Olá!! Tudo certo? Temos um sistema da forma , com posto . Portanto, será consistente se e somente se o posto . Como se reduz a
O sistema será consistente se e somente se , e , onde e podem assumir quaisquer valores.
Resposta
Veja a resolução completa.
Exercícios de Livros Relacionados
Prove que a multiplicação de matrizes é uma operação associativa: m n p = m ( n p ) .
Efetuada a mudança de eixos dada pela matriz do exercício anterior (sem mover a origem), determine os ângulos que cada um dos novos eixos forma com o antigo. m = 1 7 2 6 x 3 2 y 6 - 3 z
Seja m uma matriz ortogonal 3 x 3 . Se m . x = d , onde x = x y z ed = d 1 d 2 d 3 , Prove que d 1 2 + d 2 2 + d 3 2 = x 2 + y 2 + z 2 .
Suponha que a mudança de coordenadas x , y , z → x ' , y ' , z ' se exprima matricialmente por x ' = m . ( x - u ) , que a mudança x ' , y ' , z ' → x ' ' , y ' ' , z ' ' seja dada por x ′ = n · (x ′
Considere as seguintes afirmações sobre uma matriz m do tipo 3 × 3:a) As linhas de m são os vetores unitários mutuamente ortogonais; b) m . m T = I 3 ; c) As colunas de m são vetores unitários mutuame