Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 8.2 - Ex. 6

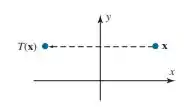
Conforme indicado na figura, seja o operador linear que reflete cada ponto no eixo .

Encontre o núcleo de .

será injetora? Justifique sua resposta.

Passo 1

Belezinha então galerinha, vamos primeiro encontrar a matriz que representa essa reflexão em torno do eixo , e a partir dela a gente consegue encontrar o núcleo e verificar se é injetora ou não.

Passo 2

Como a transformação é uma reflexão em torno do eixo , isso quer dizer que tudo que é ortogonal a esse eixo, no caso o eixo , é refletido, e tudo que está no eixo permanece intacto. Logo podemos representar essa transformação como .

Passo 3

Dado que a transformação é vamos ter uma matriz . E a partir de extraímos que

Passo 4

Na letra (a), pediram pra gente encontrar o núcleo de , que nada mais é do que a solução do sistema . Resolvendo para

Logo, , e nosso núcleo é a solução trivial .

Passo 5

Na letra (b), como temos que , nossa matriz vai ser injetora.

Resposta

.
é injetora.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostrar que cada um dos operadores lineares do R 3 a seguir é inversível e determinar o isomorfismo inverso em cada caso:(a )F ( x ,y ,z )=( x-3 y-2 z ,y-4 z ,z ) ; (b) F ( x ,y ,z )=( x ,x -y ,2 x+y-

Mostrar que cada um dos operadores lineares do R 3 a seguir é inversível e determinar o isomorfismo inverso em cada caso:(a )F ( x ,y ,z )=( x-3 y-2 z ,y-4 z ,z ) ; (b) F ( x ,y ,z )=( x ,x -y . ,2 x+

Considere o operador linear F do R 3 definido por F ( 1 ,0 ,0 )=( 1 ,1 ,1 ) , F ( 0 ,1 ,0 )=( 1 ,0 ,1 ) eF 0 ,1 ,2=( 0 ,0 ,4 ) . F é invertíıvel? Se for, determine o isomorfismo inverso.

Provar que o R 2 é isomorfo a qualquer sub-espaço de dimensão 2 do R 3 .

Seja F :R 3 → R 3 definida por F ( 1 ,0 ,0 ) = ( 1 ,1 ,0 ) e F ( 0,0 ,1 )=( 0 ,0 ,2 ) e F 0 ,1,0 = ( 1 ,1 ,2 ). Determinar uma base de cada um dos seguintes sub-espaços vetoriais: K e r ( F ), I m ( F