Exercícios de Injetividade, Sobrejetividade e Bijetividade de uma TL - Lista de Exercícios Resolvida

Seja e definida por . Mostre que é injetiva.

Seja transformação linear injetivas.

Prove que se são vetores linearmente independentes, então os vetores são também linearmente independentes.

Seja uma .

é sobrejetiva se, e somente se:

é injetiva se, e somente se:

Dada a transformação abaixo:

Ache uma base para a imagem de e a sua dimensão;

Verifique se é bijetiva.

Sejam e espaços vetoriais de dimensão finita e uma transformação linear. Considere as seguintes afirmações:

se é injetora, então

se , então é injetora;

se é sobrejetora, então

Assinale a alternativa correta:

apenas as afirmações e são necessariamente verdadeiras;

apenas a afirmação é necessariamente verdadeira;

apenas as afirmações e são necessariamente verdadeiras;

apenas as afirmações e são necessariamente verdadeiras;

todas as afirmações são necessariamente verdadeiras.

Seja a transformação linear definida por:

Assinale a alternativa correta:

é sobrejetora;

;

Seja a transformação linear definida por:

Assinale a alternativa correta:

é injetora;

é sobrejetora;

Seja E um espaço vetorial de dimensão finita com produto interno, seja S um subespaço não trivial de E e seja o operador linear definido por , para todo . Então pode-se afirmar corretamente que

Sejam e seja : o operador linear que satisfaz , . Então, T é injetor se, e somente se, for

À questão “Dado fixo, a transformação dada por é linear?”, Andrezinho respondeu da seguinte maneira:

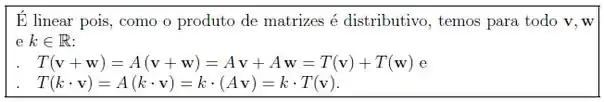
Embora seja realmente uma transformação linear, a justificativa do Andrezinho não está correta. Qual foi o erro que ele cometeu?

Mostre que é linear.

Existe algum tal que seja injetiva?

Determine uma base do núcleo e uma base da imagem de quando

Seja uma transformação linear dada por:

(a) Determine uma base para o núcleo de T. T é injetora?

Sejam e duas transformações lineares injetivas.

Prove que se são vetores linearmente independentes, então os vetores são também linearmente independentes.

Classifique as afirmativas abaixo onde é uma matriz tal que :

– não pode ser injetiva.

– não pode ser sobrejetiva.

a) Ambas são falsas.

b) é verdadeira e é falsa.

c) Ambas são verdadeiras.

d) é falsa e é verdadeira.

e) Não sei.

Considere as bases

Dos espaços vetoriais e , respectivamente. Sejam e a transformação linear tal que:

Temos que é injetora se, e somente se:

Escolha uma opção:

A única transformação linear abaixo que NÃO é INJETIVA é:

1. Uma projeção sobre a reta em .
2. Uma rotação radianos em torno da reta em .
3. Um cisalhamento em .
4. A reflexão através da reta em .

Seja a transformação linear dada por:

E sejam e bases para e respectivamente.

Prove que é isomorfismo.

Responda:

Seja linear tal que e Determine Determine uma base e diga se é sobrejetora.

A transformação associada à matriz

a)é bijetiva

b)não é nem sobrejetiva, nem injetiva

c) é sobrejetiva

d)é injetiva

Seja dada por

1. Determine uma base para
2. Determine uma base para
3. é injetora? Justifique
4. é sobrejetora? Justifique

Seja o espaço dos polinômios da forma e seja a transformação derivada, . Defina , onde denota a transformação identidade em .

1. é injetiva.
2. é sobrejetiva.

é verdadeira e é falsa

é falsa e é verdadeira

é falsa e é falsa

é verdadeira e é verdadeira

Q13. Sejam e a transformação linear tal que:

e .

Temos que será injetora se, e somente se, for diferente de :

a) 4;

b) 3;

c) 2;

d) 1;

e) 0.

Seja uma transformação linear. Sabendo que e assinale a afirmativa FALSA:

(a) não é sobrejetiva.

(b)

(c) não é injetiva.

(d) , para todo

(e) Não sei.

Seja o espaço dos polinômios

Qual função abaixo NÃO é uma função injetiva de em ?

Seja uma transformação linear de em . Assinale a afirmativa VERDADEIRA:

Se é inversível, então é injetiva, mas não é sobrejetiva.

Se é sobrejetiva, então é invertível, mas não é injetiva.

Se é injetiva, então é inversível, mas não é sobrejetiva.

Se é invertível, então é injetiva e sobrejetiva.

Seja a transformação linear dada por , e base de .

c) Determine uma base para o é sobrejetora?

Seja uma transformação linear dada por:

(b) Determine uma base para a imagem de T. T é sobrejetora?

Considere uma transformação linear , um conjunto e sua imagem . Considere as afirmativas:

1. Se é linearmente independente e é injetiva então também é linearmente independente.
2. Se é gerador de e é injetiva então é gerador de .

1. (I) é falsa e (II) é verdadeira.
2. (I) é verdadeira e (II) é verdadeira.
3. (I) é verdadeira e (II) é falsa.
4. (I) é falsa e (II) é falsa.

09) Sejam e considere a transformação linear definida por:

para quaisquer . Assinale a alternativa correta:

a) será injetora se, e somente se, ;

b) será injetora se, e somente se, ;

c) será sobrejetora se, e somente se, ;

d) será bijetora se, e somente se, ;

e) será sobrejetora se, e somente se, .

08) Considere as seguintes afirmações:

existe uma transformação linear tal que:

se for um espaço vetorial de dimensão finita e for uma transformação linear tal que , então:

existe uma transformação linear bijetora .

Assinale a alternativa correta:

a) apenas as afirmações e são verdadeiras.

b) todas as afirmações são falsas;

c) apenas a afirmação é verdadeira;

d) apenas as afirmações e são verdadeiras;

e) apenas a afirmação é verdadeira.

Seja o sistema linear .

Considere as afirmativas:

1. Se é injetiva então possui solução e a solução é única
2. Se é sobrejetiva então possui solução e a solução é única.

1. I é falsa e II é verdadeira
2. I é verdadeira e II é falsa
3. I é falsa e II é falsa
4. I é verdadeira e II é verdadeira

Sejam e números reais, uma base de , uma base de e a transformação linear tal que:

Pode-se afirmar que:

1. será injetora se, e somente se, ou ;
2. será injetora se, e somente se, e ;
3. é injetora;
4. será injetora se, e somente se, e ;

Considere o produto .

(I) Se é injetiva, então é injetiva.

(II) Se , então

(a) Ambas as afirmações são falsas.

(b) Ambas as afirmações são verdadeiras.

(c) (I) é falsa e (II) é verdadeira.

(d) (I) é verdadeira e (II) é falsa.

Sejam U e V espaços vetoriais de dimensão finita e seja uma transformação linear. Assinale a alternativa que contém uma implicação que é necessariamente verdadeira.

10) Sejam e a transformação linear tal que:

Temos que será injetora se, e somente se:

a) ;

b) ;

c) ;

d) ;

e) .

02) Seja a transformação linear definida por:

para quaisquer . Assinale a alternativa a correta:

a) é injetora;

b)

c) é sobrejetora;

d)

e) .

06) Sejam um inteiro positivo, um espaço vetorial de dimensão e uma transformação linear. Considere as seguintes afirmações:

1. será injetora se, e somente se, for sobrejetora;
2. será injetora se, e somente se, for injetora;
3. Se for uma base do espaço vetorial , então a dimensão de coincidirá com a dimensão do subespaço vetorial de gerado pelas linhas da matriz .

Assinale a alternativa correta:

a) apenas a afirmação (III) é necessariamente verdadeira;

b) apenas as afirmações (I) e (II) são necessariamente verdadeiras;

c) apenas as afirmações (II) e (III) são necessariamente verdadeiras;

d) apenas a afirmação (I) é necessariamente verdadeira;

e) apenas a afirmação (II) é necessariamente verdadeira.

A respeito das afirmações

.

A transformação linear abaixo que é sobrejetiva é:

1. A projeção ortogonal sobre o plano em
2. A projeção ortogonal sobre a reta do
3. Um cisalhamento em
4. A projeção sobre a reta do , seguida de uma reflexão sobre o eixo em

Qual das transformações abaixo representa uma transformação linear SOBREJETIVA?