Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.4 - Ex. 6
Considere dois sistemas de coordenada no sistema , em que o sistema é obtido do sistema por uma rotação do ângulo em torno do eixo , Determine a relação entre as coordenadas, , em relação ao sistema e , em relação ao sistema .
Passo 1
Eaew, belezinha?
A primeira coisa a se fazer é lembrar que uma rotação de um sistema de coordenadas em duas dimensões, ocorre da seguinte forma:
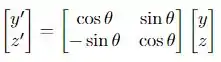
Aqui eu escolhi como exemplos simplesmente porque o enunciado diz que a rotação ocorre ao redor do eixo . Nós precisamos generalizar isso para o caso pedido no enunciado, beleza?
Passo 2
Temos a seguinte situação generalizada:
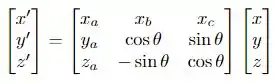
O ponto aqui é analisar esta matriz e identificar o valor dos parâmetros que foram adicionados! Note que temos uma rotação em torno do eixo , como discuti no passo 1. Portanto, a relação entre as coordenadas com as e , devem ser que nem a que está no passo (1), saca só o que obtemos se fizermos o produto matricial!
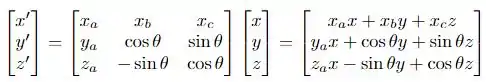
Nós obtemos um sistema de equações lineares! Portanto, para que isso tenha equivalência ao sistema anteriormente estabelecido, é preciso que , obtendo:
Beleza, vamos achar os parâmetros que faltam!
Passo 3
Agora, vamos usar a informação de que o vetor de base se manteve inalterado, portanto, temos que:
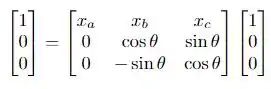
Desta forma, é necessário que . No entanto, e ? Nas condições estabelecidas acima eles indicam translações da origem do sistema de coordenadas, como a origem se mantém, temos que . Temos então no fim das contas:
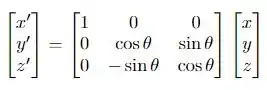
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos