Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 8.9 - Ex. 21

Dez pares de observações foram feitas das variáveis x e y , resultando no gráfico abaixo.

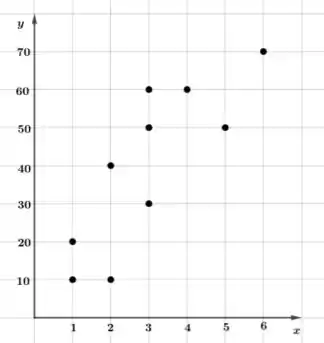
  1. Qual é a correlação entre as duas variáveis?
  2. Se as unidades do eixo-x fossem 10, 20 etc., qual seria a correlação?

Passo 1

  1. Do estudo da estatística, sabemos que o coeficiente de correlação entre as duas variáveis é dado por:

    2. r = ∑ i = 1 10 ( x i - x - ) ( y i - y - ) ∑ i = 1 10 x i - x - 2 ∑ i = 1 10 y i - y - 2

    O conjunto de dados é:

    { 1,10 , 1,20 , 2,10 , 2,40 , 3,30 , 3,50 , 3,60 , 4,60 , 5,50 , 6,70 }

    Assim, temos que:

    x - = 1 + 1 + 2 + 2 + 3 + 3 + 3 + 4 + 5 + 6 10 = 3

    y - = 10 + 20 + 10 + 40 + 30 + 50 + 60 + 60 + 50 + 70 10 = 40

    Passo 2

    Vamos calcular o numerador:

    ∑ i = 1 10 x i - x - y i - y - =

    = 1 - 3 10 - 40 + 1 - 3 20 - 40 + 2 - 3 10 - 40 + 2 - 3 40 - 40 + 3 - 3 30 - 40 + 3 - 3 50 - 40 + 3 - 3 60 - 40 + 4 - 3 60 - 40 + 5 - 3 50 - 40 + 6 - 3 70 - 40 = 260

    Logo:

    ∑ i = 1 10 x i - x - y i - y - = 260

    Passo 3

    Agora vamos calcular o denominador:

    ∑ i = 1 10 x i - x - 2 = 1 - 3 2 + 1 - 3 2 + 2 - 3 2 + 2 - 3 2 + 3 - 3 2 + 3 - 3 2 + 3 - 3 2 + 4 - 3 2 + 5 - 3 2 + 6 - 3 2 = 24

    ∑ i = 1 10 y i - y - 2 =

    = 40 - 10 2 + 20 - 40 2 + 10 - 40 2 + 40 - 40 2 + 30 - 40 2 + 50 - 40 2 + 60 - 40 2 + 60 - 40 2 + 50 - 40 2 + 70 - 40 2 = 4200

    Queremos:

    24 ∙ 4200 = 120 7

    Passo 4

    Agora é só fazer a conta:

    r = 26 0 120 7 ≅ 0 , 82

    Passo 5

  2. Note que ele multiplicou todas as variáveis do eixo x por 10 . As grandezas lineares vão sofrer esta mesma variação:

10 x - = 30

∑ i = 1 10 10 x i - 10 x - y i - y - = 10 ∑ i = 1 10 x i - x - y i - y - = 260 0

∑ i = 1 10 10 x i - 10 x - 2 = 100 ∑ i = 1 10 x i - x - 2 = 2400

Disso, temos que:

∑ i = 1 10 x i - x - 2 ∑ i = 1 10 y i - y - 2 = 2400 ∙ 4200 = 10 ∙ 120 7

Note então que:

r = 10 ∙ 260 10 ∙ 120 7 ≅ 0,82

Ou seja, a correlação permanece a mesma.

Resposta

  1. 0,82 ;
  2. Não muda.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os dados abaixo representam a produção de soja durante vários anos em um determinado terreno. Utilizando seus conhecimentos teóricos, experimentais e bom senso, faça uma previsão da produção em 1980 .
A definição de espaço vetorial complexo foi dada na primeira nota marginal da S e ç ã o4.1 çã . A definição de um produto interno complexo num espaço vetorial complexo V é idêntica à definição1 , exce
Use a Fórmula 4 para mostrar que u , v = 9 u 1 v 1 + 4 u 2 v 2 é o produto interno em R 2 gerado por A = 3 00 2 Use o produto interno da parte a para calcular u , v com u = - 3,2 e v = 1,7 .
Mostre que vale a identidade dada com vetores de qualquer espeço com produto interno. u + v 2 + u - v 2 = 2 u 2 + 2 v 2