Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 1.2 - Ex. 4

Achar uma matriz diagonal semelhante à matriz

([[3,-,1,-,1],[-,6,1,2],[2,1,0]])

Passo 1

Nós temos

A = ([[3,-,1,-,1],[-,6,1,2],[2,1,0]])

Vamos usar a formulazinha para descobrir os valores próprios

det ( A - I lambda ) = 0

Lembrando que I é a matriz identidade e o lambda é o valor que queremos descobrir, logo

I = ([[1,0,0],[0,1,0],[0,0,1]]) e I lambda = ([[lambda,0,0],[0,lambda,0],[0,0,lambda]])

Passo 2

Vamos subtrair

(- [[3,-,1,-,1],[6,1,2],[2,1,0]]) - ([[lambda,0,0],[0,lambda,0],[0,0,lambda]]) = ([[3,-,lambda,-,1,-,1],[-,6,1,-,lambda,2],[2,1,-,lambda]])

Certinho? Então descobrimos A - I lambda , agora falta colocar no determinante!

|[[3,-,lambda,-,1,-,1],[-,6,1,-,lambda,2],[2,1,-,lambda]]| [[3,-,lambda,-,1],[-,6,1,-,lambda],[2,1]]

A equação característica é

4 lambda^2 - lambda^3 + 3 lambda - 2 ->

Ixi, temos uma equação de 3º grau! Você pode resolver o sistema da maneira que você achar melhor, nós vamos diminuir um grau da equação!

Passo 3

Primeiro, vamos começar com o chute pra ver se descobrimos uma raiz precisamos que quando substituir seja igual a zero!

f (lambda) = 4 lambda^2 - lambda^3 + 3 lambda - 2

:.

f (2) = 4 xx 2^2 - 2^3 + 3 xx 2 - 2 -> 12 != 0

f (1) = 4 xx 1^2 - 1^3 + 3 xx 1 - 2 -> 4 != 0

f (- 1) = 4 ( - 1 )^2 - (- 1)^3 + 3 (- 1) - 2 -> 0 = 0

Olha, encontramos uma raiz! E para baixar o grau, aplicaremos o Briot Rufini! Se você nunca ouviu falar, presta atenção na explicação!

Vamos fazer um quadro, na primeira linha colocamos os coeficientes na equação, na linha abaixo colocaremos a raiz que encontramos

- lambda^3 + 4 lambda^2 + 3 lambda - 2

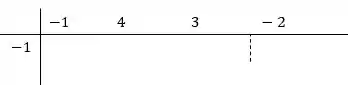
Primeira coisa é repetir o primeiro coeficiente. Depois, multiplicamos ele pelo - 1 e somamos com o segundo coeficiente (4). A resposta, colocamos embaixo do 4 e repetimos esse processo até o último coeficiente (2). Beleza??

Fica assim no final:

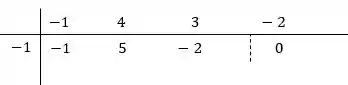
Assim, pegando os valores dentro da caixinha, entre -1 e -2, a nossa equação de 2º é

- 1 lambda^2 + 5 lambda - 2

Agora vamos para o Bháskara!

Delta = b^2 - 4 a c -> 5^2 - 4 (- 1) (- 2) = 17

Então, teremos as raízes:

lambda_2 = (5 - sqrt(17))/(2)

E

lambda_3 = (5 + sqrt(17))/(2)

Passo 4

Agora, vamos achar os vetores próprios!

Para lambda_1 = - 1 :

([[3,-,1,-,1],[-,6,1,2],[2,1,0]]) ([[x],[y],[z]]) = - ([[x],[y],[z]])

Que nos dá o sistema:

{[[3 x - y - z = - x],[- 6 x + y + 2 z = - y],[2 x + y = - z]])

{[[4 x - y - z = 0],[- 5 x + y + 2 z = 0],[2 x + y + z = 0]])

Resolvendo o sistema, chegamos no vetor:

([[x],[y],[z]]) = ([[0],[0],[0]])

Para lambda_2 = (5 - sqrt(17))/(2) = 0,44 :

([[3,-,1,-,1],[-,6,1,2],[2,1,0]]) ([[x],[y],[z]]) = 0,44 ([[x],[y],[z]])

Que nos dá o sistema:

{[[3 x - y - z = 0,44 x],[- 6 x + y + 2 z = 0,44 y],[2 x + y = 0,44 z]])

Resolvendo o sistema, chegamos no vetor:

([[x],[y],[z]]) = ([[0],[0],[0]])

Para lambda_3 = (5 + sqrt(17))/(2) = 4,56 :

([[3,-,1,-,1],[-,6,1,2],[2,1,0]]) ([[x],[y],[z]]) = 4,56 ([[x],[y],[z]])

Que nos dá o sistema:

{[[3 x - y - z = 4,56 x],[- 6 x + y + 2 z = 4,56 y],[2 x + y = 4,56 z]])

Resolvendo o sistema, chegamos no vetor:

([[x],[y],[z]]) = ([[0],[0],[0]])

Eita, como encontramos a matriz:

M = [[[0,0,0],[0,0,0],[0,0,0]]]

Não possuímos uma resposta...

Resposta

Não existe resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Demonstre que se A e B são semelhantes, então possuem os mesmos polinômios característicos e portanto os mesmo autovalores.
Demonstre que A e A t possuem os mesmos autovalores. O que podemos dizer sobre os autovetores de A e A t .
Mostre que se A e B são matrizes ortogonais, então AB é ortogonal.
Verifique se a matriz cos ⁡ θ - sin ⁡ θ sin ⁡ θ cos ⁡ θ é ortogonal.
Mostre que se A é uma matriz ortogonal, então det ⁡ A = ± 1 .