Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 1.2 - Ex. 5a

Estudar quanto à possibilidade de diagonalização as matrizes

1 2 - 2 2 1 - 2 2 2 - 3

Passo 1

Nós temos

A = 1 2 - 2 2 1 - 2 2 2 - 3

Vamos usar a formulazinha para descobrir os valores próprios

det ⁡ ( A - I λ ) = 0

Lembrando que I é a matriz identidade e o λ é o valor que queremos descobrir, logo

I = 1 0 0 0 1 0 0 0 1         e   I λ = λ 0 0 0 λ 0 0 0 λ

Passo 2

Vamos subtrair

1 2 - 2 2 1 - 2 2 2 - 3 - λ 0 0 0 λ 0 0 0 λ = 1 - λ 2 - 2 2 1 - λ - 2 2 2 - 3 - λ

Certinho? Então descobrimos A - I λ , agora falta colocar no determinante!

1 - λ 2 - 2 2 1 - λ - 2 2 2 - 3 - λ 1 - λ 2 2 1 - λ 2 2  

A equação característica é

- λ 2 - λ 3 + λ + 1

Passo 3

Primeiro, vamos começar com o chute pra ver se descobrimos uma raiz precisamos que quando substituir seja igual a zero!

f 1 = - 1 2 - 1 3 + 1 + 1 → 0 = 0

Olokinho meu! Logo de cara descobrimos uma das raízes. E para baixar o grau, aplicaremos o Briot Rufini! Se você nunca ouviu falar, presta atenção na explicação!

Vamos fazer um quadro, na primeira linha colocamos os coeficientes na equação, na linha abaixo colocaremos a raiz que encontramos

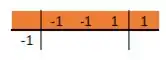
Copiamos o primeiro coeficiente. Depois, multiplicamos a raiz, o número anterior e somamos o próximo coeficiente

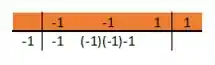
E continuamos

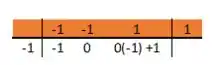
Até acabar com os espaços em branco

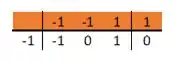
Assim, o que está entre a raiz e o zero é a nossa equação de 2º grau

- λ 2 + 1

Resolvendo

λ 2 = 1 → λ = ± 1

Encontramos os valores próprios!

Passo 4

Vamos pro vetor próprio usando λ 1 = 1

1 - λ 2 - 2 2 1 - λ - 2 2 2 - 3 - λ = 0 2 - 2 2 0 - 2 2 2 - 4

Colocando no sisteminha de equações

0 2 - 2 2 0 - 2 2 2 - 4 x 1 x 2 x 3 = 0 0 0

Assim a matriz estendida é

0 2 - 2 0 2 0 - 2 0 2 2 - 4 0

Simplificando

1 0 - 1 0 0 1 - 1 0 0 0 0 0

x 1 - x 3 = 0 x 2 - x 3 = 0 x 3 = t → x 1 = x 3 x 2 = x 3 x 3 = t → x 1 = t x 2 = t x 3 = t

Logo o vetor é

1 1 1

Passo 5

1 - λ 2 - 2 2 1 - λ - 2 2 2 - 3 - λ = 2 2 - 2 2 2 - 2 2 2 - 2

Colocando no sisteminha de equações

2 2 - 2 2 2 - 2 2 2 - 2 x 1 x 2 x 3 = 0 0 0

Assim a matriz estendida é

2 2 - 2 0 2 2 - 2 0 2 2 - 2 0

Simplificando

1 1 - 1 0 0 0 0 0 0 0 0 0

x 1 + x 2 - x 3 = 0 x 2 = s x 3 = t → x 1 = x 3 - x 2 x 2 = s x 3 = t → x 1 = t - s x 2 = s x 3 = t

Logo o vetor é

t 1 0 1     e       s - 1 1 0

Passo 6

Juntando os autovalores, teremos a matriz

1 0 0 0 - 1 0 0 0 - 1

Assim, colocando os autovetores na indicação dos autovalores, temos M igual a

M = - 2 - 4 2 3 2 1 0 1 1 1

Resposta

M = 1 1 - 1 1 0 1 1 1 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja A uma matriz n × n diagonalizável. Mostre que o traço de A é igual à soma das raízes do seupolinômio característico, incluindo as multiplicidades. (Sugestão: use o fato de que t r ( A B ) = t r (
Seja λ um autovalor da matriz não-singular A com autovetor associado X . Mostre que 1 / λ é um autovalor de A - 1 com autovetor associado X .
Uma matriz A é chamada nilpotente se A k = 0 ̄ , para algum inteiro positivo k . Reveja o Exercício 1.1.29 na página 27. Demonstre que se A é nilpotente, então o único autovalor de A é 0. (Sugestão: u
Mostre que se V é autovetor de A , então V é autovetor de A k . Com qual autovalor?
Dizemos que uma matriz B , n × n , é semelhante a uma matriz A , n × n , se existir uma matriz P não singular tal que B = P - 1 A P . Demonstre:(a) A é semelhante a A ;(b)Se A é semelhante a B , então