Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 7d
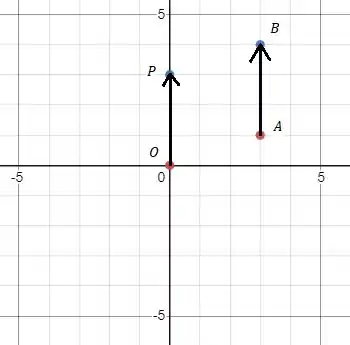
Construir o gráfico correspondente a cada situação. Representar em um gráfico o vetor e o correspondente vetor posição, nos casos:
e
Passo 1
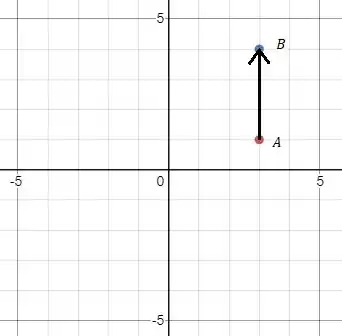
Vamos lá, temos que o vetor é representado como tendo origem no ponto e extremidade no ponto , assim vamos ligar os dois pontos para ter o vetor, vamos ver ele no gráfico abaixo:
Passo 2
Agora vamos lembrar que um vetor tem infinitos representantes, que são os segmentos orientados de mesmo comprimento, mesma direção e mesmo sentido.
E entre todos esses infinitos representantes do vetor temos o vetor posição , que tem origem em e extremidade em , onde e .
Aqui vamos então primeiro achar o ponto para poder representar o vetor posição no gráfico:
Pronto, vamos agora representar o vetor posição no nosso gráfico:
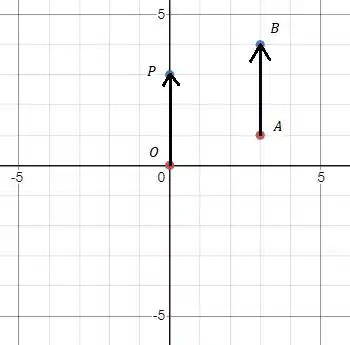
Resposta
Exercícios de Livros Relacionados
Determinar a extremidade do segmento que representa o vetor v → = 2 ,- 5 , sabendo que sua origem é o ponto A - 1 ,3 .
Dados os vetores u → = 3 ,- 1 e v → = - 1 ,2 , determinar o vetor w → tal que 3 w → - 2 v → - u → = 2 4 w → - 3 u →
Dados os vetores u → = 3 ,- 1 e v → = - 1 ,2 , determinar o vetor w → tal que 4 u → - v → + 1 3 w → = 2 u → - w →
Dados os pontos A - 1,3 , B 2 ,5 e C 3 ,- 1 , calcular O A → - A B → , O C → - B C → e 3 B A → - 4 C B →
Prove que X é um ponto interior ao triângulo de vértices A , B e C se, e somente se, existem α e β tais que α0 , β0 , α + β1 e C X → = α C A → + β C B → (um ponto é interior a um triângulo se é interi