Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 5
Prove que é um ponto interior ao triângulo de vértices , e se, e somente se, existem e tais que , , e (um ponto é interior a um triângulo se é interior a um segmento que tem por extremidades um vértice e um ponto interior ao lado oposto.)
- pertence à reta se, e somente se, existem e tais que e ;
- pertence ao segmento se, e somente se, existem e tais que , , e ;
- é interior ao segmento (isto é, existe tal que e ) se, e somente se, e são de sentido contrário.
Passo 1
Bom, vamos começar fazendo um desenho esquemático do que está acontecendo e de todas as informações que precisaremos. Portanto,
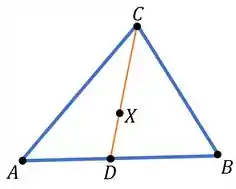
O que fizemos foi desenhar tudo que a questão nos disse. Primeiro, um triângulo de vértices , e . Depois, um ponto interior . Por fim, ela nos disse que um ponto é interior se é interior a um segmento que tem extremidades um vértice e um ponto interior ao lado oposto (lado ).
Sacaram? Escolhemos exatamente nesta ordem para utilizarmos o mesmo raciocínio (inclusive com a nomenclatura) da questão anterior, a questão 5-4.
Passo 2
Feita todas as definições iniciais, vamos as nossas relações. Como pertence ao segmento , temos:
Sendo . Continuando, o mesmo acontecerá com o ponto . Portanto,
Sendo . O que devemos fazer é escrever como combinação linear de e . Para isto, vamos escrever como combinação destes vetores primeiramente. Portanto,
Portanto, o vetor será:
Se chamarmos e , temos:
E chegamos a nossa relação. O ponto só será interior ao triângulo se existir um ponto interior ao segmento e assim teremos a relação .
Para finalizarmos, só falta provar a restrição e . Como e , automaticamente, e . Além disto,
E agora acabamos de provar tudo que a questão nos pediu!
Resposta
Ei, a resposta está no passo a passo :)