Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 19

Dado um tetraedro OABC, tem-se O A → = a → , O B → = b → , O C → = c → , O P → = 2 3 O B → . M é o ponto médio de A B → , N é o ponto médio de B C → e Q é o ponto médio de A C → . Pede-se u → = P M → + P N → + P Q → em função de a → , b → e c → .

Passo 1

Fala, galera! Essa questão exige um pouco mais de visão espacial, mas calma. Vamos começar desenhando as informações que estão no enunciado. O resultado final vai ficar como no desenho abaixo. Um tetraedro é uma pirâmide de base triangular. O A → = a → , O B → = b → , O C → = c → são os vetores que saem do topo da pirâmide e O P → = 2 3 O B → indica que P está a 2 3 do caminho entre O e B. Depois disso, identificamos os pontos médios M, N e Q, que estão nas arestas da base. Agora, podemos desenhar os vetores P M → , P N → e P Q → . Para a imagem não ficar com muitas informações, nós omitimos os nomes dos vetores.

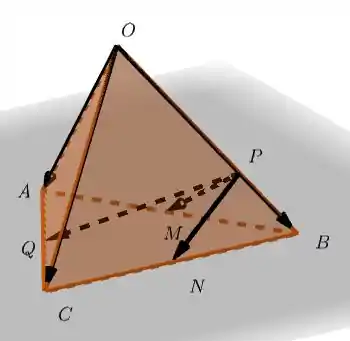
Passo 2

Agora, vamos tentar escrever P M → , P N → e P Q → em função de a → , b → e c → . Vamos começar com os dois primeiros pq são mais simples. Na figura abaixo, vemos dois lados do tetraedro.

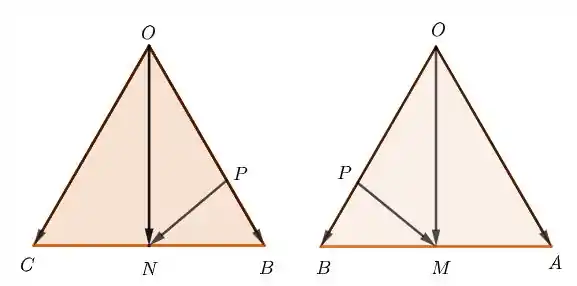
Assim, fica fácil entender que P N → = P O → + O N → = - O P → + O N → . Nós já sabemos que O P → = 2 3 O B → = 2 3 b → porque essa informação foi dada no enunciado. Falta determinar O N → . Para isso, temos que lembrar que N é ponto médio B C → , então podemos usar o resultado do Exercício Resolvido 3:

O N → = 1 2 O C → + 1 2 O B → = 1 2 c → + 1 2 b →

Assim,

P N → = - O P → + O N → = - 2 3 b → + 1 2 c → + 1 2 b → = - 1 6 b → + 1 2 c →

Para obter P M → vamos seguir o mesmo raciocínio:

P M → = - O P → + O M → = - 2 3 b → + 1 2 a → + 1 2 b → = - 1 6 b → + 1 2 a →

Para obter P Q → vamos usar um raciocínio um pouco diferente. Vamos escolher caminho POQ e calcular O Q → usando também o resultado do Exercício Resolvido 3. Nesse caso,

P Q → = P O → + O Q → = - O P → + O Q → = - 2 3 b → + 1 2 a → + 1 2 c →

Passo 3

Agora temos todas as informações necessárias para obter u → = P M → + P N → + P Q → . Assim,

u → = P M → + P N → + P Q → = - 1 6 b → + 1 2 a → - 1 6 b → + 1 2 c → - 2 3 b → + 1 2 a → + 1 2 c → = - b → + a → + c →

Resposta

u → = a → - b → + c →

Exercícios de Livros Relacionados

Sem usar coordenadas, explique o significado das seguintes afirmações: (a) os vetores u ,v são ortogonais; (b) o vetor v é ortogonal a reta r; (c) o vetor v é ortogonal ao plano Π ; (d) os vetores uev
Dados u=( α ,β ,γ ) , v=( α',β ',γ ') e w=( β γ '-γ β ',γ α '-α γ ',α β '-β α ') , calcule os produtos internos u , w ; v , w . Que relação entre u e v implica w = 0?
Sejam v 1 ,v 2ev 3 vetores não-coplanares. Se o vetor w é tal que w , v 1 = w , v 2 ≥ w , v 3 ≥ 0 , prove que w=0 .
Verifique que A=( 0 ,a / 2 ,0 ) , B=( 0 ,- a / 2 ,0 ) , C=( 0 ,0 ,a √3 / 2 ) e D=( a√6 / 3 ,0 ,a √3 / 6 ) são os vértices de um tetraedro regular A B C D . Em seguida mostre que duas arestas opostas q
Dados os números a ,b ,c ,α ,β ,γ , mostre que se tem a desigualdade ( a α + b β +c γ )2≤( a² + b ²+ c ² ) ( α²+ β ² + γ ² ) ² ² ² ² ² ² , valendo a igualdade se, e somente se, existe k tal que α=k a