Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 23

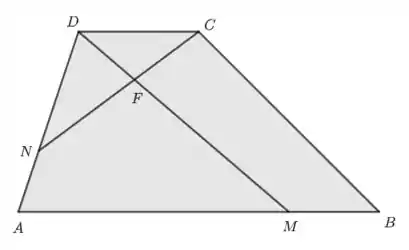
No trapézio ao lado, vec D C = (1)/(3) vec A B , vec A N = (1)/(3) vec A D , vec A M = (3)/(4) vec A B e vec C F = alpha vec C N . Determine alpha .

Passo 1

Tudo bem, galera? Prontos para mais uma resolução? Então vamos que vamos! O próprio enunciado nos diz que vec C F = alpha vec C N , mas também podemos notar que vec D F = beta vec D M . A razão para isso vai ficar mais clara daqui a pouco. Vamos tentar escrever esses dois vetores em termos de vec A B e vec A D . Primeiramente, temos que notar que

vec A D = vec A N + vec N D => vec N D = vec A D - vec A N = vec A D - (1)/(3) vec A D = (2)/(3) vec A D

Então,

vec C N = vec C D + vec D N = - vec D C - vec N D = - (1)/(3) vec A B - (2)/(3) vec A D

e

vec D M = vec D A + vec A M = - vec A D + (3)/(4) vec A B

Passo 2

Usando os dois resultados acima, podemos obter vec C F de duas formas:

vec C F = alpha vec C N = alpha (- (1)/(3) vec A B - (2)/(3) vec A D)

vec C F = vec C D + vec D F = - vec D C + beta vec D M = - (1)/(3) vec A B + beta (- vec A D + (3)/(4) vec A B) = - beta vec A D + ((3 beta)/(4) - (1)/(3)) vec A B .

Como os dois resultados devem ser iguais, então podemos escrever:

alpha (- (1)/(3) vec A B - (2)/(3) vec A D) = - beta vec A D + ((3 beta)/(4) - (1)/(3)) vec A B => ((3 beta)/(4) - (1)/(3) + (alpha)/(3)) vec A B = (beta - (2 alpha)/(3)) vec A D

Como vec A B e vec A D não são paralelos, a única forma da equação acima ser verdadeira é se ambos lados forem nulos. Os vetores claramente não são nulos, então concluímos que os coeficientes devem ser nulos. Assim,

beta - (2 alpha)/(3) => beta = (2 alpha)/(3)

(3 beta)/(4) - (1)/(3) + (alpha)/(3) = 0 => (3)/(4) (2 alpha)/(3) - (1)/(3) + (alpha)/(3) = (alpha)/(2) - (1)/(3) + (alpha)/(3) = (5 alpha)/(6) - (1)/(3) = 0 => (5 alpha)/(6) = (1)/(3) => alpha = (1)/(3) (6)/(5) = (2)/(5)

Resposta

alpha = (2)/(5)

Exercícios de Livros Relacionados

Utilizando identidades apropriadas, onde necessário, determine quais dos conjuntos de vetores em F ( - ∞ ,∞ ) dados são linearmente dependentes.b) x , cos ⁡ x
Seja A uma matriz n×n e sejam v 1 ,v 2 ,...,v n vetores linearmente independentes em R n expressos como matrizes n×1 . Para ter A v 1 ,A v 2 ,...,A v n linearmente independentes, o que A deve satisfaz
(a)Expresse ( 4 a ,a -b ,a +2 b ) como uma combinação linear de ( 4 ,1 ,1 ) e ( 0 ,- 1 ,2 ) .(b)Expresse ( 3 a +b +3 c ,- a +4 b -c ,2 a +b +2 c ) como uma combinação linear de ( 3 ,- 1 ,2 ) e ( 1 ,4
(a) Expresse v=( 1 ,1 ) como uma combinação linear de v 1=( 1 ,- 1 ) ,v 2=( 3 ,0 ) e v 3=( 2 ,1 ) de duas maneiras distintas.(b) Explique por que isso não contradiz o Teorema 4.4 . 1
16 No tetraedro ABCD, sejam M, N e P, respectivamente, os pontos médios de BD, CD, e AC, e G o baricentro do triângulo MNP.Exprima B G → como combinação linear de B A → ,B C → ,B D → . Calcule m para