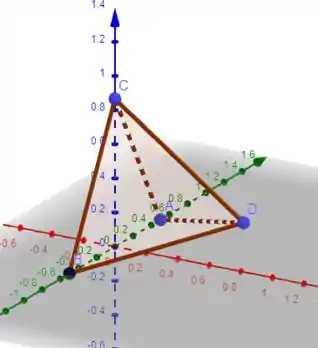
Verifique que , e ) são os vértices de um tetraedro regular . Em seguida mostre que duas arestas opostas quaisquer como, por exemplo, AC e BD, são ortogonais.

Saudações galerinha, tudo bem?

Vamos começar a resolver mais um exercício, bora lá então!

Inicialmente começaremos plotar esses, supondo ,temos o nosso tetraedro.

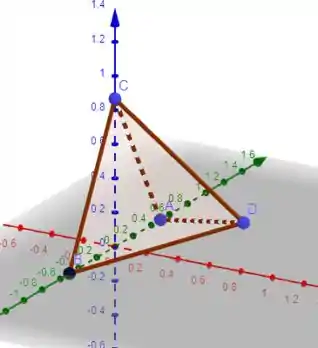
Vamos agora provar que seus lados são ortogonais.

Seja um tetraedro tal que , .

Precisamos provar .

Então teremos ,

Desta forma

E que

Prontinho!

Acabamos te vejo na próxima questão!