Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 13a
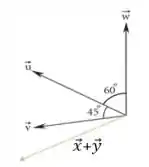
13. Dado os vetores coplanares , e representados na Figura 1.36 determinar:
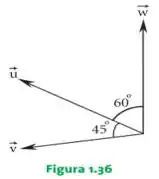
a) Um representante do vetor , sendo e .
Passo 1
Então pessoal, para representarmos o vetor temos que seguir alguns passos, tudo bem? O primeiro passo consiste em determinarmos a primeira soma vetorial: , o segundo passo consiste em determinarmos a segunda soma vetorial: e, por fim, o terceiro e último passo consiste em somarmos . Sendo assim, vamos devagarinho pra não surgir nenhuma dúvida ou complicação, tudo bem? Show!
Para determinarmos essa soma devemos utilizar a seguinte regrinha: unir a setinha do primeiro vetor com a traseira do segundo vetor. Um exemplo disso seria:
Vamos considerar esses dois vetores quaisquer. A soma entre eles, utilizando a regrinha supracitada, seria:
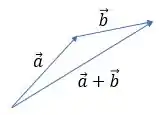
E é essa a ideia que vamos utilizar aqui, tudo bem? Então bora que bora!
Passo 2
A primeira soma vetorial que devemos fazer é . Desenhando esses dois vetores de acordo com a figura que nos foi dada, teremos algo assim:
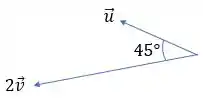
Utilizando a regrinha do passo anterior, o vetor soma seria:
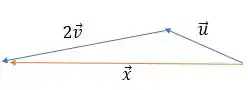
A segunda soma vetorial que devemos fazer é . Utilizando a regrinha do passo anterior, o vetor soma seria:
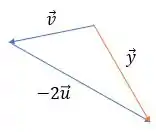
Ok, dois passos já foram concluídos, agora vamos finalizar o terceiro!
Passo 3
O queremos determinar, na verdade, é , certo? De acordo com os nosso resultados do passo anterior, esses vetores ficaram da seguinte maneira:
Utilizando a regrinha para determinar essa soma, teremos como resultado:
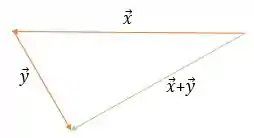
E esse é o representante do vetor , galera! 😉
Resposta
Representante do vetor :
