Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 13b
13. Dado os vetores coplanares , e representados na Figura 1.36 determinar:
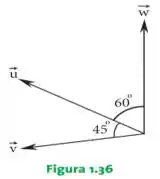
b) O ângulo entre os vetores e .
Passo 1
Então galera, a questão quer que descubramos o ângulo formado pelos vetores e , mas como fazemos isso? Vamos analisar o que muda em cada um dos vetores, se liga:
No vetor aparece um sinal de negativo e um escalar multiplicando o vetor, certo? O sinal de negativo implica que estamos mudando o SENTIDO do vetor , galera. Diferentemente disso, temos que o escalar está fazendo com que o TAMANHO do vetor aumente. Em resumo teremos um vetor em sentido oposto e vezes maior, tudo bem?
Já no vetor não mudamos nada, então ele continua do mesmo jeito, assim como na figura! Esboçando nossos novos vetores:
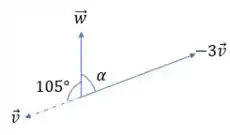
Show!
Passo 2
Galera, note que agora queremos encontrar o valor de , que é exatamente o ângulo entre nossos novos dois vetores, tudo bem? De acordo com o que estudamos em trigonometria, temos que meia volta numa circunferência vale , não é mesmo? Sendo assim, pelo desenho do passo anterior, temos o seguinte:
E esse é o ângulo entre nossos dois novos vetores, pessoal!
Resposta
O ângulo é de .