Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 4

A B C D é um quadrilátero, A D → = 3 v → ,   B C → = 2 v →   e A B → = w → . Que tipo de quadrilátero é A B C D ? Determine o lado C D → e as diagonais B D → e A C → em função de v → e w → .

Passo 1

Fala ae, galera! Blz? 😊

Vamos analisar a imagem abaixo para entender bem o problema

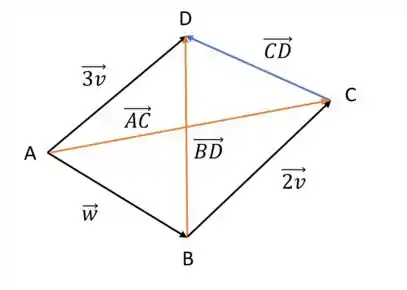
Passo 2

Precisamos definir quem é o vetor C D → .

Pela adição de vetores, temos que:

C D → = - 2 v → - w → + 3 v → = v → - w →

Passo 3

Agora, vamos definir as diagonais.

Diagonal A C → :

A C → = w → + 2 v →

Diagonal B D → :

B D → = - w → + 3 v →

Já que todos os lados do quadrilátero possuem lados cujos valores são diferentes, temos que A B C D é um paralelogramo irregular.

Resposta

A B C D : P a r a l e l o g r a m o   I r r e g u l a r .

C D → = v → - w →

A C → = w → + 2 v →

B D → = - w → + 3 v →

Exercícios de Livros Relacionados

Sejam s 1 e t 1 duas retas concorrentes em B, tangentes à circunferência de centro A e raio r 1 , (Figura 5-10). Com centro em um ponto P da semi-reta de origem B que contém A, traça-se a circunferênc
(b) Sejam OABC um tetraedro e X o baricentro do triângulo ABC. Exprima O X → em função de O A → , O B → e O C → .
Dado o triângulo ABC não retângulo, a = t g ,  b = t gB ^ e c = t gC ^ .Sendo CX a altura relativa ao vértice C, prove que a A X → = b X B → e exprima C X → em função de C A → ,C B → ,a ,b .
Dado o triângulo ABC, seja X a interseção do lado AB com a bissetriz do ângulo interno de vértice C (Figura 5-8) e sejam a = | | C B → | | e b = | | C A → | | .Explique geometricamente por que C X → é
Dado o triângulo da Figura 5-8, sejam a = | | C B → | | e b = | | C A → | | suponhamos que a ≠ b . Seja Y a intersecção da reta AB com a bissetriz do ângulo externo do vértice C.d) O que ocorreria se