Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 19.Problemas - Ex. 9

Dados os dois focos de uma hipérbole e a distância entre os vértices, achar a equação da mesma.

Passo 1

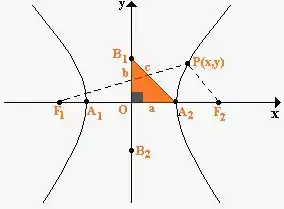
Oiii gente! Bom nesse problema temos que lembrar da característica principal da hipérbole: A diferença entre as distâncias de um ponto P x , y para ambos os focos F 1 − c , 0 e F 2 c , 0 é sempre constante. Lembrando disso, agora podemos dar início a nossa questão. Adotaremos que a d P , F 1 − d P , F 2 = 2 a .

Para determinar a equação do ramo direito da hipérbole, reescrevemos a última relação dessa forma :

d P , F 1 = d P , F 2 + 2 a

x + c ² + y ² = x − c ² + y ² + 2 a

Elevando a equação ao quadrado:

x + c ² + y ² = x − c ² + y ² + 4 a x − c ² + y ² + 4 a ²

x ² + 2 c x + c ² + y ² = x ² − 2 c x + c ² + y ² + 4 a ² + 4 a x − c ² + y ²

4 c x − 4 a ² = 4 x − c ² + y ²

c x − a ² = x − c ² + y ²

Simplificando a equação:

c ² − a ² x ² − a ² y ² = a ² c ² − a ²

Passo 2

Bom, pela figura acima se encontra que b ² = c ² − a ² , uma vez que se trata de um triângulo retângulo. Substituindo essa relação na equação anterior, temos:

c ² − a ² x ² − a ² y ² = a ² c ² − a ²

b ² x ² − a ² = a ² b ²

x ² a ² − y ² b ² = 1

É importante destacar também que esse mesmo raciocínio se repete para o ramo esquerdo da hipérbole.

E aí, essa resolução te ajudou?

Bons Estudos!

Resposta

Resolução nos passos acima

Exercícios de Livros Relacionados

Nos problemas 50 a 53, obter uma equação geral da hipérbole dada por equações paramétricas. Esboçar o gráfico. x = 2 + 3t gθ y = 1 + 4 sec ⁡ θ
Nos problemas 50 a 53, obter uma equação geral da hipérbole dada por equações paramétricas. Esboçar o gráfico. x = t gθ y = 3 sec ⁡ θ
Nos problemas 50 a 53, obter uma equação geral da hipérbole dada por equações paramétricas. Esboçar o gráfico. x = 2 sec ⁡ θ y = 4 + 3 t gθ
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.focos F 0 , ± 3 , vértices A 0 , ± 2
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.focos F 0 , ± 4 , eixo real de medida 2