Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Hipérbole - Ex. 52

Nos problemas 50 a 53, obter uma equação geral da hipérbole dada por equações paramétricas. Esboçar o gráfico.

x = 2 + 3   t g   θ y = 1 + 4 sec ⁡ θ

Passo 1

E aí, tudo belezinha?

Vamos relembrar como são as paramétricas:

  • Eixo paralelo ao eixo x : a equação reduzida é da forma: x - h 2 a 2 - y - k 2 b 2

    • e aí as paramétricas vão ser:

    x = h + a sec ⁡ θ y = k + t g   θ

  • Eixo paralelo ao eixo y : a equação reduzida é da forma: y - k 2 a 2 - x - h 2 b 2

e aí as equações paramétricas vão ser da forma:

x = h + b   t g   θ y = k + a sec ⁡ θ  

Daí a gente pode fazer o caminho reverso...

Passo 2

A gente tem:

x = 2 + 3   t g   θ y = 1 + 4 sec ⁡ θ

Daí, com as relações do passo 1 , a gente conclui que essa hipérbole tem:

e i x o   p a r a l e l o   a o   y

c e n t r o = ( 2,1 )

a = 4

b = 3

Juntando os ingredientes acima, escrevemos nossa equação reduzida:

y - 1 2 4 2 - x - 2 2 3 2 = 1

y - 1 2 16 - x - 2 2 9 = 1

Passo 3

Só que o problema não quer a equação reduzida, e sim a geral! (ô cara exigente hein?!)...

Então vamos desenvolver essa equação:

9 y - 1 2 144 - 16 x - 2 2 144 = 1

9 y - 1 2 - 16 x - 2 2 = 144

9 y 2 - 2 y + 1 - 16 x 2 - 4 x + 4 = 144

9 y 2 - 18 y + 9 - 16 x 2 + 64 x - 64 = 144

9 y 2 - 16 x 2 - 18 y + 64 x - 199 = 0

Agora sim! Essa é a equação geral da hipérbole!

Passo 4

Nos falta agora esboçar o gráfico, que vai ficar assim:

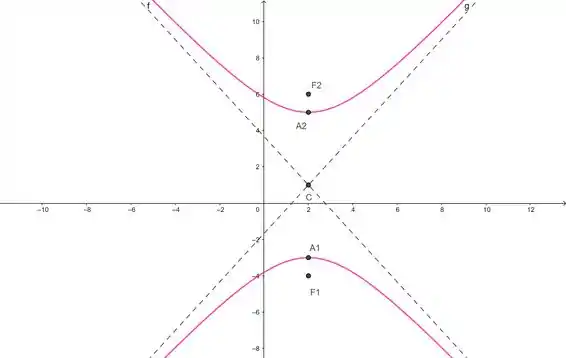
E agora acabamos! 😉

Resposta

9 y 2 - 16 x 2 - 18 y + 64 x - 199 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Focos F 1 - 1 , - 5 eF 2 ( 5 , - 5 ) e que seja hipérbole equilátera.
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( 2 , - 3 ) , eixo real paralelo a O y e passando por ( 3 , - 1 )
Em cada um dos problemas 38 a 43, determinar a equação reduzida, o centro, os vértices, os focos, a excentricidade e equações das assíntotas das hipérboles dadas. Esboçar o gráfico. 9 x 2 - 4 y 2 - 18
Em cada um dos problemas 38 a 43, determinar a equação reduzida, o centro, os vértices, os focos, a excentricidade e equações das assíntotas das hipérboles dadas. Esboçar o gráfico. x 2 - 4 y 2 + 6 x
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( - 2,1 ) , eixo real paralelo a O x e passando por ( 0,2 ) e ( -