Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 17a

Dados os vetores u → = ( 3 , - 1 ,   2 ) e v → = ( - 2 ,   2 ,   1 ) , calcular:

a) a área do paralelogramo determinado por u → e v → ;

Passo 1

Primeiro, vamos fazer um esboço do nosso paralelogramo:

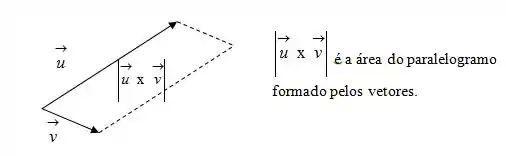
Passo 2

Dado u → = ( 3 , - 1 ,   2 ) e v → = ( - 2 ,   2 ,   1 ) , a área do paralelogramo determinado por u → e v → pode ser dada por u → × v → , assim, mão na massa!

u → × v → = i → j → k → 3 - 1 2 - 2 2 1 = - i → - 4 j → + 6 k → - 4 i → + 3 j → + 2 k → = - 5 i → - 7 j → + 4 k →

u → × v → = - 5 2 + - 7 2 + 4 2 = 90 = 3 10

Portanto, a área do paralelogramo determinado por u → e v → é 3 10 . 😉

Resposta

A área do paralelogramo é 3 10 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove a identidade de Lagrange V × W 2 = V 2 W 2 - V ⋅ W 2 .
O produto vetorial é associativo? Justifique sua resposta. (Sugestão: experimente com os vetores i → , j → , k → )
Se V × W = V × U e V ≠ 0 - , então W = U ?
Sejam U 1 , U 2eU 3 três vetores unitários mutualmente ortogonais. Se A = U 1 U 2 U 3 é uma matriz 3 × 3 cujas colunas são os vetores U 1 , U 2eU 3 , então A é invertível e A - 1 = A t . (Sugestão: mo
a) Prove que A × B × C + B × C × A + C × A × B = 0 (Sugestão: use o exercício anterior).