Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 6.Exercícios Propostos - Ex. 2

A , B , C e D são vértices consecutivos de um paralelogramo, sendo A   =   ( 1 , - 3,2 ) , B =   ( 0,6 , - 3 ) e C   =   ( 5,1 , 4 ) .

  1. Determine as coordenadas do ponto D
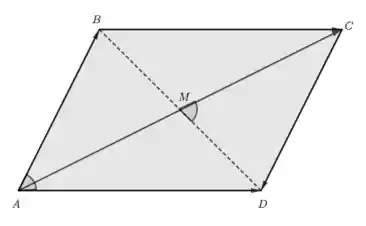
  2. Mostre que as diagonais A C → e B D → têm o mesmo ponto médio.

Passo 1

  1. E aí, jovens? Para determinar o ponto D, temos que notar que temos um paralelogramo, ou seja, lados opostos tem mesmo tamanho. Assim

    2. D C → = A B → = B - A = ( 0,6 , - 3 ) - ( 1 , - 3,2 ) = ( - 1,9 , - 5 )

    Por outro lado,

    D C → = C - D

    então

    D = C - D C → = ( 5,1 , 4 ) - ( - 1,9 , - 5 ) = ( 6 , - 8,9 )

    Passo 2

  2. Para mostrar que as diagonais A C → e B D → têm o mesmo ponto médio. Vamos supor que as diagonais não tenham o mesmo ponto médio e que seus pontos médios são M e N .

Assim, temos que mostrar que

A M → = A B → + B N →

porque isso quer dizer que M = N .

Vamos começar escrevendo

A M → = 1 2 A C → = 1 2 ( A B → + B C → )

Além disso,

B N → = 1 2 B D → = 1 2 ( B C → + C D → ) = 1 2 ( B C → - D C → ) = 1 2 ( B C → - A B → )

Vamos substituir esse resultado na equação:

A B → + B N → = A B → + 1 2 ( B C → - A B → ) = 1 2 ( A B → + B C → ) = A M →

Que é justamente o que queríamos mostrar.

Resposta

  1. D = ( 6 , - 8,9 )
  2. Veja a resolução acima.

Exercícios de Livros Relacionados

Ainda com A = 2 . - 1eB = ( 5,1 ) , o ponto P tem abcissa x e AP é perpendicular a AB. Qual é a ordenada de P?
Tomando no plano um sistema de eixos oblíquos no qual o ângulo de OX para OY é θ , mostre que a distância do ponto P = x , y ao ponto P ' = x ' , y ' é dada por d P , P ' = x - x ' 2 + y - y ' 2 + 2 x
Tome, sobre as retas A BeA C do exercício anterior, pontos PeQ tais que d A , P = d A , Q . Ache o ponto médio M do segmento P Q e obtenha a equação da reta A M , bissetriz do ângulo B Â C . Â
Qual é a equação da circunferência que passa pelos pontos A = (1, 2), B = (3, 4) e tem o centro sobre o eixo OY?
Com os mesmos dados do primeiro exercício, obtenha as coordenadas do centro P = (x, y) da circunferência ABC resolvendo o sistema de equações d(A, P)² = d(B, P)² e d(B, P)² = d(C, P)², nas incógnitas