Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 15b
Sendo e o ângulo entre e , calcular
b)
Passo 1
Neste problema, sabendo que os vetores e o ângulo entre e precisamos calcular , certo?
Então, vamos lá? Aposto que vocês conseguem!
Passo 2
Primeiro, vamos fazer um esboço do nosso problema:
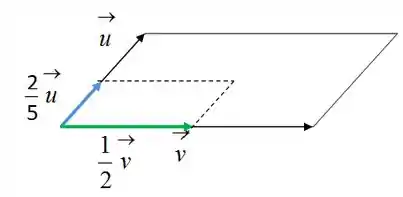
Temos que , certo? Então, basta substituir os valores dados que matamos a questão, hehe.
Passo 3
Assim, fazendo o cálculo, temos:
Passo 4
Por fim, basta multiplicarmos os vetores pelos seus respectivos escalares dados na questão. Assim, temos que:
Portanto, . 😉
Resposta
Exercícios de Livros Relacionados
Sendo w → = ( u → + 2v → ) ^ ( u → + v → ) , determine o ângulo dos vetores u → e v → , sabendo que u → = v → = w → = 2 e u → ⋅ v →0 .
Determine a área do paralelogramo ABCD cujas diagonais são A C → = 0,2 , 3 e B D → = - 2,4 , 1 .
Sendo u → = - 1,1 , m ,v → = 7,5 , 1ew → = a , b , c , pede-se:O valor de m para que a equação v → = u → ^ w → possa ter solução;Para o valor de m encontrado em a), resolva a equação v → = u → ^ w → ,
Dados u → = ( 1,2 , - 1 ) e v → = ( 1,3 , - 2 ) , determine um vetor a → , ortogonal a u → e a v → , de módulo 3 e que forma com k → um ângulo obtuso.
Sejam O A → = 1,3 , - 1 ,O B → = 0,2 , - 1 eO C → = 3,4 , 2 .Calcule a área do triângulo ABC.Determine um vetor x → , de módulo 1, perpendicular ao plano ABC. Desenhe um representante de x → . Desenha