Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 1.Problemas Propostos - Ex. 1d
Dados os vetores e da figura, mostrar num gráfico, um representante do vetor
Passo 1
Vamos primeiro desenhar os vetores e .
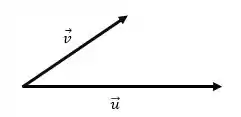
Passo 2
Temos o vetor dado como o vetor com o dobro do tamanho e o vetor que é como o vetor com o triplo do tamanho só que no sentido contrário. Então:
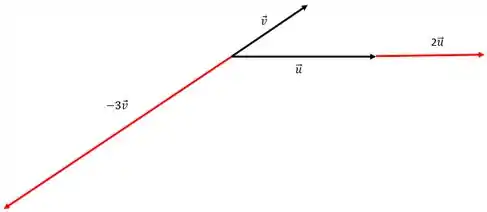
Passo 3
Vamos usar da regra do paralelogramo para resolver essa questão.
Desconsiderando o vetor , temos:
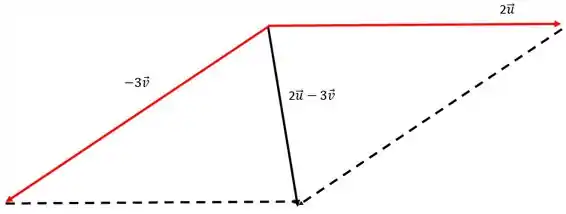
Resposta
Exercícios de Livros Relacionados
Na Figura 5.9, A M → = 2 M B → e 3 A N → = N C → . Exprima X em função de A, A B → , A C → .
Sejam A, B e C vértices de um triângulo.Prove (algebricamente) que não existe o ponto X quando m +n = 0 . E interprete geometricamente este caso.
Os segmentos AN, BP e CM são dois a dois não paralelos. Dê uma condição necessária e suficiente sobre os vetores A N → , B P → e C M → , que não envolva suas normas, para que exista um triângulo de la
Sejam A , B e C pontos quaisquer, A ≠ B . Prove que: X pertence à reta A B se, e somente se, existem α e β tais que C X → = α C A → + β C B → e α + β = 1 ; X pertence ao segmento A B se, e somente se,
O ponto X divide A , B na razão α , Y divide B , C na razão β e Z divide C , A na razão γ . Exprima C X → , A Y → e B Z → em função de C A → , C B → , α , β , γ .