Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 3.2 - Ex. 26
Demonstre que as diagonais de um losango são perpendiculares.
Passo 1
Vamos primeiro visualizar o problema, temos um losango tal que:
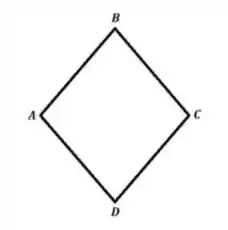
Dessa forma, por soma de vetores, sabemos que as diagonais do losango são:
Passo 2
Para provarmos que as diagonais e são ortogonais, precisamos mostrar que o produto interno dos dois vetores é 0. Assim:
Pela distributiva:
Reorganizando a conta:
Passo 3
Dado que os vetores estão elevados ao quadrado, podemos dizer que:
Ou seja:
Como podemos conferir pela figura, e são ambos lados do losango, ou seja, possuem o mesmo comprimento, a mesma norma, logo:
Resposta
Como o produto interno dos vetores da diagonal do losango é igual a 0, as diagonais são ortogonais.
Exercícios de Livros Relacionados
Seja o cubo de aresta a representado na Figura 2.17 . Determinar: E D → ⋅ A B → O G →
Calcular os ângulos diretores do vetor vec v = (6 , - 2,3) .
Determinar um vetor unitário ortogonal ao eixo O z e que forme 60 ° com o vetor i → .
O vetor v → é ortogonal aos vetores u → = 1,2 , 0 e w → = 2,0 , 1 e forma ângulo agudo com o vetor j → . Determinar v → , sabendo que v → = 21 .
Determinar o vetor a → de módulo 5 , sabendo que é ortogonal ao eixo O y e ao vetor v → = i → - 2 k → , e forma ângulo obtuso com o vetor i → .