Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 31f

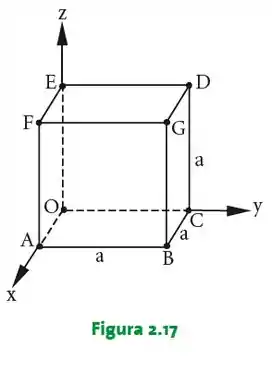
Seja o cubo de aresta a representado na Figura 2.17 . Determinar:

E D → ⋅ A B → O G →

Passo 1

Primeiro vamos encontrar os vetores E D → , A B → e O G → :

E D → = D - E

A B → = B - A

O G → = G - O

Temos então que achar os pontos D , E , B , A , G e O de acordo com a figura:

D = 0 , a , a

E = 0,0 , a

B = a , a , 0

A = a , 0,0

G = a , a , a

O = 0,0 , 0

Passo 2

Agora sim vamos então encontrar os vetores:

E D → = D - E = 0 , a , a - 0,0 , a = 0 - 0 , a - 0 , a - a = 0 , a , 0

A B → = B - A = a , a , 0 - a , 0,0 = a - a , a - 0,0 - 0 = 0 , a , 0

O G → = G - O = a , a , a - 0,0 , 0 = a - 0 , a - 0 , a - 0 = a , a , a

Passo 3

Pronto, agora vamos calcular o produto escalar, mas primeiro vamos ver como que se calcula.

Chama-se produto escalar de dois vetores u → = x 1 , y 1 , z 1 e v → = x 2 , y 2 , z 2 , representado por u → ⋅ v → , o número real encontrado pela seguinte soma:

u → ⋅ v → = x 1 x 2 + y 1 y 2 + z 1 z 2

Vamos aplicar agora na nossa questão:

E D → ⋅ A B → = 0 , a , 0 ⋅ 0 , a , 0 = 0 ⋅ 0 + a ⋅ a + 0 ⋅ 0 = a 2

E por último vamos fazer a multiplicação do escalar pelo vetor:

E D → ⋅ A B → O G → = a 2 a , a , a = a 2 ⋅ a , a 2 ⋅ a , a 2 ⋅ a = a 3 , a 3 , a 3

Resposta

E D → ⋅ A B → O G → = a 3 , a 3 , a 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o vetor unitário com mesma direção e sentido que o vetor dado. 9 , - 5
Determine o vetor unitário com mesma direção e sentido que o vetor dado. 12 i - 5 j
Determine a soma dos vetores dados e ilustre geometricamente. - 1 , 0 , 2 , ⟨ 0 , 4 , 0 ⟩
Determine a soma dos vetores dados e ilustre geometricamente. 3 , - 1 , ⟨ - 2,4 ⟩
Determine a soma dos vetores dados e ilustre geometricamente. 0,1 , 2 , ⟨ 0,0 , - 3 ⟩