Demonstre que as diagonais de um paralelogramo se cortam ao meio. (Sugestão: Sejam M e N os pontos médios das duas diagonais do paralelogramo. Mostre que o vetor , então conclua que M = N).
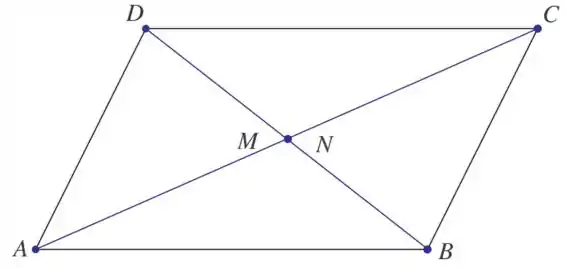
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de geometria analítica.
Para responder ao questionamento do enunciado, usamos a seguinte equação vetorial:
Da figura temos que:
Reescrevendo a equação vetorial temos que:
E como os vetores que temos são simétricos, e sabemos que:
Teremos que:
Logo, M = N.
Resposta
Ver passo a passo.