Deseja-se construir um circuito como o mostrado na figura,

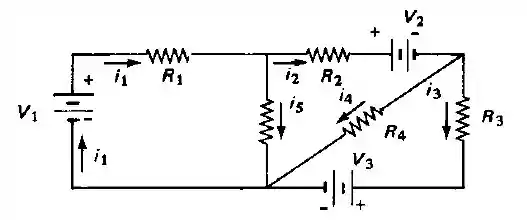
Onde , , , , , , , .

Dispõe-se de uma tabela de preços de vários tipos de resistências; assim como as correntes máximas que elas suportam sem queimar.

De que tipo devemos escolher cada resistência para que o circuito funcione com segurança e a sua fabricação seja a de menor custo possível?

Para começar vamos ter que montar equações para representar nosso circuito e para isso vamos utilizar as leis dos nós, que diz para gente que a corrente que entra em um nó tem que ser igual as correntes que saem desse mesmo nó.

Usando as leis dos nós obtemos as equações:

Agora teremos que aplicar a lei das malhas que diz para a gente que a soma das diferenças de potencial de uma malha tem que ser igual a 0.

Aplicando a lei das malhas obtemos as equações:

Repara só que no sistema da lei dos nós temos duas linhas que são linearmente dependentes (a segunda e a terceira), então podemos montar um novo sistema só com uma delas e o resto das linhas:

Onde teremos 5 incógnitas para 5 equações. Vamos achar uma solução de boa.

Agora que já montamos nosso sistema, vamos para parte que estamos mais acostumados e vamos escrever a matriz ampliada associada ao sistema:

Vamos tentar simplificar nosso sistema usando operações de multiplicação e soma em linha para reduzir a matriz à forma escada, então vamos começar aquela série de operações que usamos para simplificar nossa matriz:

Primeiro fazendo :

Agora :

Trocando :

Fazendo

Trocando

Fazendo :

Agora :

Fazendo

Agora

Respira porque agora vamos subir...

Fazendo

Agora :

E :

Fazendo

E, finalmente,

Pronto, depois de todas essas transformações podemos reescrever nosso sistema na forma:

Fazendo essas continhas:

Agora vamos ver quais os valores na tabela.

- Como a passa pela resistência de , então:

- Como a passa pela resistência de , então:

- Como a passa pela resistência de , então:

- Como a passa pela resistência de , então:

- Como a passa pela resistência de 10, então:

Somando tudo: