Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 14.4 - Ex. 4

Quais são os vértices da região poliedral convexa em R 2 , definida por

x ≥ 0 2 x + 3 y ≤ 2 3 x + 2 y ≤ 2 x + y ≤ 1

Desenha esta região.

Passo 1

Pra desenhar a região, é mais fácil se a gente botar só o y pra um lado. Isso vai facilitar pra analisarmos se o espaço que a gente quer está abaixo ou acima das retas!

x ≥ 0 2 x + 3 y ≤ 2 3 x + 2 y ≤ 2 x + y ≤ 1

Desenvolvendo,

x ≥ 0 → d i r e i t a   d o   e i x o   y y ≤ - 2 3 x + 2 3 → a b a i x o y ≤ - 3 2 x + 1 → a b a i x o y ≤ - x + 1 → a b a i x o

Passo 2

Os vértices vão ser os pontos de encontro das retas! Vamos igualar duas a duas.

Os vértices com x = 0 são:

x = 0 → y = 2 3

x = 0 → y = 1

x = 0 → y = 1

O último foi repetido!

E os vértices do encontro das três retas são os seguinte:

Da primeira e da segunda,

- 2 x 3 + 2 3 = - 3 x 2 + 1

5 6 x = 1 3

x = 2 5 → y = 2 5

Da segunda e terceira,

- 3 x 2 + 1 = - x + 1

x = 0 → y = 1

Da terceira e primeira,

- 2 x 3 + 2 3 = - x + 1

x = 1 → y = 0

Daí, os vértices são:

1 ,   0 ,   0 ,   1 ,   2 5 , 2 5 ,   0 , 2 3

Passo 3

Beleza, agora é só a gente traçar as retas e pegar os espaços acima ou abaixo delas! A região que queremos vai ser o que está dentro dos quatro espaços!

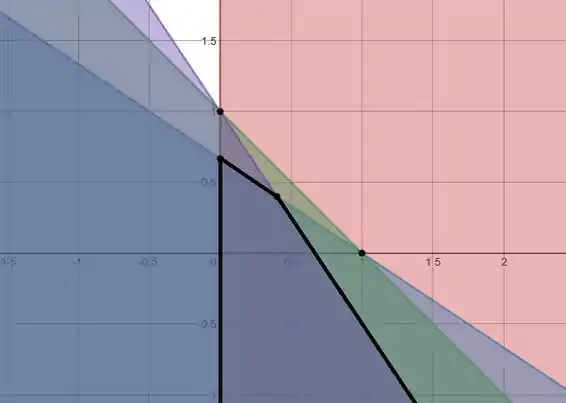
Então fechou! Nossa região vai ser tudo aquilo dentro da região preta, que se estende atééééé lá embaixo, infinitamente.

Resposta

Vértices:

1 ,   0 ,   0 ,   1 ,   2 5 , 2 5 ,   0 , 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe a região em R 2 , definida pelas desigualdades 2 x + y + 9 ≥ 0 - x + 3 y + 6 ≥ 0 x + 2 y - 3 ≤ 0
Seja f x ,y = 3 x + 3 y definida na região poliedral convexa abaixo:Qual o valor máximo e mínimo de f ?Calcule os valores f ( A ) , f ( B ) e f ( P ) , onde P é um ponto no segmento A B .Use ( a ) e (
Uma máquina produz dois tipos A e B de frascos de vidro, mas não simultaneamente. Ao produzir um frasco do tipo A ela gasta 0,2 horas, e ao produzir um tipo B , gasta 0,4 horas. Sabendo que a máquina
Na definição de variedade linear em 14.2 . 1 , prove que v 0 ∈ A . O vetor v 0 é único? W é único? Interprete geometricamente.