Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 6.Problemas Propostos - Ex. 12c
Determinar a distância da reta
c) ao eixo dos
Passo 1
Vamos começar encontrando uma equação vetorial pra nossa reta. Temos que e , então:
Beleza, essa reta passa pelo ponto e tem vetor diretor .
Passo 2
O eixo dos é uma reta que passa pela origem e tem vetor diretor , pois está na direção de hehe então ela tem equação
Opa, repara só: nossa reta e a reta têm o mesmo vetor diretor , então são paralelas, olha:
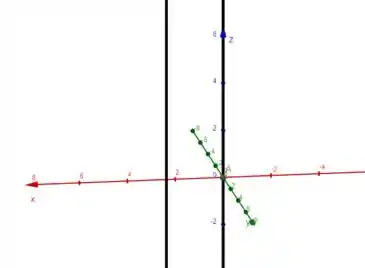
Agora é só encontrarmos a distância entre as duas retas paralelas :)
Passo 3
Para encontrar a distância entre duas retas paralelas, vamos encontrar um ponto de , depois um ponto genérico de .
Temos que um ponto de é , e um ponto genérico de , de acordo com sua equação, é
Sabendo que , para termos a menor distância, devemos ter (ou seja, o vetor deve ser ortogonal às retas).
Como , o ponto pode ser escrito como
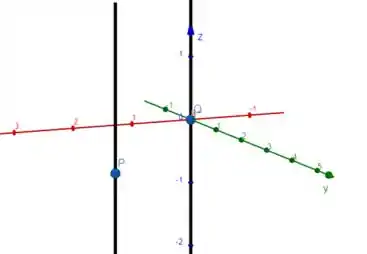
Passo 4
Bom, agora é só encontrarmos a distância entre os pontos e , usando a fórmula de distância entre pontos: