Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Hipérbole - Ex. 20
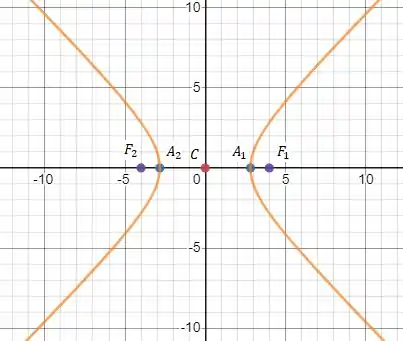
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.
Focos e que seja hipérbole equilátera
Passo 1
Vamos lá, temos que a hipérbole possuem os seguintes elementos:
- Dois focos, e , que possui uma distância focal de entre eles
- Um centro que é o ponto médio do segmento dos focos
- Dois vértices, e
- O eixo real que é o segmento com comprimento
- O eixo imaginário que é o segmento com comprimento
Aqui vemos que o vértice está no eixo , assim temos que a equação da hipérbole é com eixo real sobre , assim vai ser da forma:
Vamos então encontrar os valores , , e .
Passo 2
Pelas informações do enunciado temos que o centro é e como os focos são o valor de é , e como queremos que seja uma hipérbole equilátera devemos ter os valores de e iguais:
Para achar a equação da hipérbole só nos falta encontrar , e podemos usar a seguinte expressão:
Vamos então substituir os valores:
Pronto, agora é só substituir na expressão e temos a equação da hipérbole:
Passo 3
Vamos também encontrar os vértices para montar o gráfico, como a distância do centro aos vértices é o valor vamos ter que as coordenadas de são:
E a é constante e igual a , assim os vértices são e .
Passo 4
Agora vamos esboçar o gráfico usando a expressão da hipérbole que encontramos, :
