Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 7.5 - Ex. 9

Determinar a equação reduzida referida ao sistema X O ' Y e o gênero da cônica representada pela equação dada a seguir. Esboçar o gráfico.

3 x 2 - 2 x y + 3 y 2 - 2 x - 10 y - 1 = 0

Passo 1

Precisamos escrever a equação da cônica dada num sistema de coordenadas em que não aparece o termo misto x y . Para isso, consideremos a parte quadrática:

3 x 2 - 2 x y + 3 y 2

Ela pode ser escrita como

x y ⋅ 3 - 1 - 1 3 ⋅ x y

Vamos estudar a matriz

A = 3 - 1 - 1 3

Num sistema de coordenadas ( X , Y ) em que A for diagonal, o termo misto desaparecerá! Vamos procurar os autovalores de A :

3 - λ - 1 - 1 3 - λ = 0

Assim,

3 - λ 2 - 1 = 0

Logo,

3 - λ = ± 1

Portanto, temos

λ 1 = 2         e           λ 2 = 4

Passo 2

Agora que temos os autovalores, vamos procurar os autovetores. Para λ 1 = 2 :

1 - 1 - 1 1 ⋅ a b = 0 0 ⇒ a - b = 0 ⇒ b = a

Portanto,

u 1 = a , b = a , a = a 1 ,   1

Para que o vetor seja unitário, a = 1 / 2 :

u 1 = 1 2 , 1 2

Já para λ 2 = 4 :

- 1 - 1 - 1 - 1 ⋅ a b = 0 0 ⇒ a + b = 0 ⇒ a = - b

Logo,

u 2 = - b ,   b = b - 1 ,   1

Com b = 1 / 2 :

u 2 = - 1 2 , 1 2

Passo 3

Assim, já temos que

x y ⋅ 3 - 1 - 1 3 ⋅ x y = X Y ⋅ 2 0 0 4 ⋅ X Y = 2 X 2 + 4 Y 2

Além disso,

x y = 1 2 - 1 2 1 2 1 2 ⋅ X Y

Portanto,

x = X 2 - Y 2         e         y = X 2 + Y 2

Desta forma, a equação da cônica pode ser escrita como

2 X 2 + 4 Y 2 - 2 X 2 - Y 2 - 10 X 2 + Y 2 - 1 = 0

Logo,

2 X 2 + 4 Y 2 - 12 X 2 - 8 Y 2 - 1 = 0

Agora vamos completar quadrados:

2 X 2 - 12 X 2 = 2 X 2 - 6 X 2 + 9 2 - 9 2 = 2 X - 3 2 2 - 9

4 Y 2 - 8 Y 2 = 4 Y 2 - 2 Y 2 + 1 2 - 1 2 = 4 Y - 1 2 2 - 2

Desta forma, a equação pode ser reescrita como

2 X - 3 2 2 - 9 + 4 Y - 1 2 2 - 2 - 1 = 0 ⇒ 2 X - 3 2 2 + 4 Y - 1 2 2 = 12

Assim,

X - 3 2 2 6 + Y - 1 2 2 3 = 1

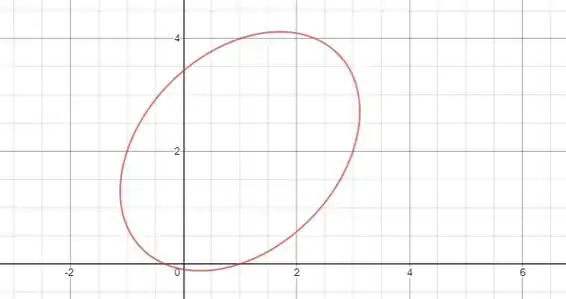
Trata-se de uma elipse, cujo gráfico é dado a seguir:

Resposta

X - 3 2 2 6 + Y - 1 2 2 3 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 9 . x y + 16 = 0
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 10 . 5 x 2 + 6 x y + 5 y 2 = 9
Nos exercícios de 13 a 22, simplifique a equação dada com uma rotação e uma translação de eixos. Faça um esboço do gráfico e mostre os três conjuntos de eixos. 15 . 17 x 2 - 12 x y + 8 y 2 - 68 x + 24
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 11 . 31 x 2 + 10 3 x y + 21 y 2 = 144
Nos exercícios de 13 a 22, simplifique a equação dada com uma rotação e uma translação de eixos. Faça um esboço do gráfico e mostre os três conjuntos de eixos. 13 . x 2 + x y + y 2 - 3 y - 6 = 0