Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 4.Problemas Propostos - Ex. 12c
Determinar as equações das seguintes retas:
c) reta que passa por e é ortogonal ao mesmo tempo ao eixo dos e dos ;
Passo 1
Já temos um ponto da reta, que é , agora precisamos de um vetor diretor.
Olha uma coisa:
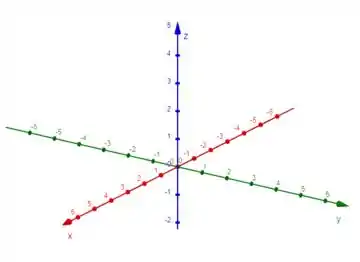
Bem, se essa reta é perpendicular ao eixo e ao eixo , ela é paralela ao eixo , ou seja, tem vetor diretor
Então vamos lá. A equação vetorial de uma reta é assim:
Onde é um ponto e é um vetor diretor.
Logo, substituindo as informações que temos, a equação da nossa reta é essa aqui:
Resposta
Exercícios de Livros Relacionados
Obter equações reduzidas na variável x , da reta:Que passa pelos pontos A ( 1 , - 2,3 ) e B ( 3 , - 1 , - 1 ) .
Na reta y = 2 x + 3 z = x - 1 determinar o ponto de:Ordenada igual a 9 ;
Determinar o ponto da reta r : x - 1 2 = y + 3 - 1 = z 4 que possui:a) Abscissa 5 .
Obter o ponto de abscissa 1 da reta r : 2 x + 1 3 = 3 y - 2 2 = z + 4 e encontrar um vetor diretor de r que tenha ordenada 2 .
Verificar se os pontos P 1 ( 5 , - 5,6 ) e P 2 ( 4 , - 1,12 ) pertencem à reta r : x - 3 - 1 = y + 1 2 = z - 2 - 2