Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 6a
6) Determinar o vetor x nas figuras:
a)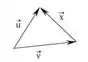 
Passo 1
O nosso primeiro passo vai ser relembrar a soma de vetores, a gente viu na teoria que ela é caracterizada desse jeitinho aqui:
Passo 2
Agora que a gente já relembrou isso dai, vamos partir para a figura da nossa questão:
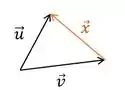
Se formos comparar essa figura com a anterior, podemos ver que o vetor é a soma dos vetores e .
Ou seja,
Como queremos :
Resposta
Exercícios de Livros Relacionados
No paralelogramo ABCD ao lado, temos D E → = αD C → , 3 B F → = F C → e G é a interseção das retas A E ̄ e D F ̄ . Determine α para termos A G → = 4 G E → ;a seguir, expresse w → = C G → como combinaç
Sejam A, B, C e D quatro pontos e M e N os pontos médios dos segmentos AC e BD. Determine, em função de M N → , a soma s → = A B →+A D→ +C B →+C D → .(Sugestão: A B →=A M→ +M N →+N B → e, analogamente
Mostre que se α V = 0 - , então α = 0 ou V = 0 - .
Mostre que se α V = 0 - , então α = 0 ou V = 0 - .
Se α U = α V , então U = V ? E se α ≠ 0 ?