Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 25

Sejam A, B, C e D quatro pontos e M e N os pontos médios dos segmentos AC e BD. Determine, em função de M N → , a soma s     → = A B →   +   A D   → +   C B →   +   C D → .

(Sugestão: A B →   =   A M   → +   M N →   +   N B → e, analogamente, para os demais vetores ou, se preferir, use o resultado do exercício resolvido 3. )

Passo 1

Ok, pessoal, a essa altura vocês já sabem qual é a primeira coisa a se fazer nessa questão. Sim, temos que fazer uma figura com as informações do enunciado.

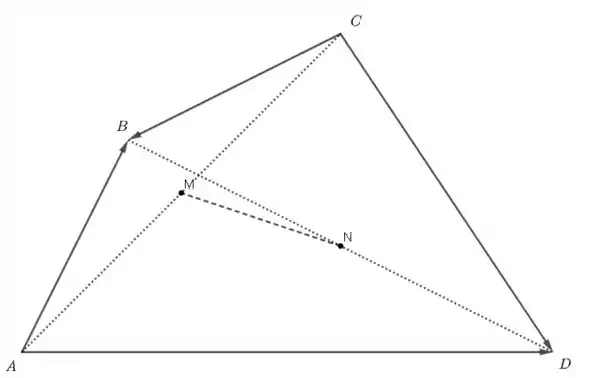
Passo 2

Seguindo a sugestão do próprio livro, vemos que

A B →   =   A M   → +   M N →   +   N B → = 1 2 A C   → +   M N →   + 1 2   D B →

onde usamos o fato de M e N serem pontos médios, ou seja, eles dividem os segmentos AC e BD em duas partes iguais. De maneira muito semelhante, podemos obter os demais vetores necessários em termos de A C   → ,   M N →   ,   D B → . Então, vamos lá!

  A D   → =   A M   → +   M N → +   N D   → = 1 2 A C   → +   M N →   + 1 2   B D → = 1 2 A C   → +   M N →   - 1 2   D B →

  C B → =   C M → +   M N → +   N B → = 1 2 C A   → +   M N →   + 1 2   D B → = - 1 2 A C   → +   M N →   + 1 2   D B →

  C D → =   C M → +   M N → +   N D → = 1 2 C A   → +   M N →   + 1 2   B D → = - 1 2 A C   → +   M N →   - 1 2   D B →

Passo 3

Agora, vamos utilizar os vetores calculados no passo anterior para obter:

s     → = A B →   +   A D   → +   C B →   +   C D →

s → = 1 2 A C   → +   M N →   + 1 2   D B → + 1 2 A C   → +   M N →   - 1 2   D B → - 1 2 A C   → +   M N →   + 1 2   D B → - 1 2 A C   → +   M N →   - 1 2   D B →

s → = ( 1 2 + 1 2 - 1 2 - 1 2 ) A C   → + ( 1 + 1 + 1 + 1 )   M N →   + ( 1 2 - 1 2 + 1 2 - 1 2 )   D B →

s → = 4 M N →

Resposta

s → = 4 M N →

Exercícios de Livros Relacionados

Dados quatro pontos quaisquer A , B , CeD no plano, ponha u = A B → , v = B C → , w = C D → , portanto u + v = A C ,v + w = B D →eu + v + w = A D → . Conclua então que A B → , C D → + A C → , D B → +
Suponha dada uma correspondência que associa a cada vetor v do plano um vetor v ' com as propriedades a), b), c) do exercício anterior. Prove que só há 3 possibilidades: ou v ' = 0 para todo v , ou v
Dados os vetores u, v, com u ≠ 0 , prove que o vetor w = v -v , u u , u. u é perpendicular a u .
Sejam u , v vetores não colineares. Se um vetor w é tal que w , u = 0 e w , v = 0 , mostre que w = 0 .
Dados a, b não simultaneamente iguais a zero, e c qualquer, o conjunto dos pontos P = x , y tais que a x + b y ≥ c é convexo.