Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.1 - Ex. 3

Determine se o conjunto equipado com as operações dadas é um espaço vetorial. Para os que não são espaços vetoriais, identifique os axiomas que falham.

O conjunto de todos os números reais com as operações padrão de adição e multiplicação.

Passo 1

Vamos lá sendo u = u 1 ,     u 2 e v = ( v 1 ,   v 2 ) .

Axioma 1: se u e v são objetos de V então a soma u + v deve ser objeto de V , isso nós chamamos que V é fechado para a soma e provamos isso na letra passada.

Axioma 2: Comutatividade.

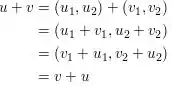
Axioma 3: Associatividade

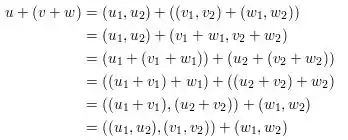
Axioma 4: Soma com vetor nulo deve ser o próprio vetor.

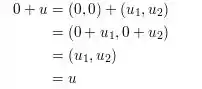
Axioma 5: u + - u = 0

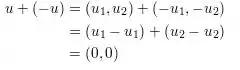
Axioma 6: Se k é um escalar está contido no conjunto dos reais então k ⋅ u está contido nos reais o que é verdade pois não podemos transacionar entre conjuntos se fizermos o produto de dois elementos contidos no mesmo conjunto.

Axioma 7:

k   ⋅ u + v = k ⋅ u + k ⋅ v

Sendo k = 2

2 ⋅ u 1 + v 1 ,   u 2 + v 2 = ( 2 u 1 + 2 v 1 ,   2 u 2 + 2 v 2 )

2 ⋅ u 1 ,   u 2 + 2 ⋅ v 1 ,   v 2 = ( 2 u 1 + 2 v 1 ,   2 u 2 + 2 v 2 )

Logo k   ⋅ u + v = k ⋅ u + k ⋅ v .

Axioma 8:

u   ⋅ k + m = k ⋅ u + m ⋅ u

Sendo k = 2 , m = 3 .

u 1 ,   u 2 ⋅ 2 + 3 = 5 u 1 ,   5 u 2

2 ⋅ u 1 ,   u 2 + 3 ⋅ u 1 ,   u 2 = 2 u 1 + 3 u 1 ,   2 u 2 + 3 u 2 = 5 u 1 ,   5 u 2

Logo   u   ⋅ k + m = k ⋅ u + m ⋅ u .

Axioma 9:

u   ⋅ k ⋅ m = k ⋅ u ⋅ m

Sendo k = 2 , m = 3 .

u 1 ,   u 2 ⋅ 2 ⋅ 3 = 2 u 1 ,   2 u 2 ⋅ 3 = 6 u 1 ,   6 u 2

u 1 ,   u 2 ⋅ 3 ⋅ 2 = 3 u 1 ,   3 u 2 ⋅ 2 = 6 u 1 ,   6 u 2

logo   u   ⋅ k ⋅ m = k ⋅ u ⋅ m .

Axioma 10:

1 ⋅ u = u

1 ⋅ u 1 ,   u 2 = u 1 ,   u 2

Logo   1 ⋅ u = u

Como todos os axiomas foram provados V é espaço vetorial.

Ufa, finalmente terminamos!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

21 Sejam u, v e w os vetores do exercício 19. Encontre os componentes do vetor x que satisfazem a equação 2u-v-x=7x+w.
23 Qual(is) dos vetores em R6 dados é(são) paralelo(s) a u= - 2 ,1 ,0 ,3 ,5,1 ? 4 ,2 ,0 ,6 ,10 ,2
23 Qual(is) dos vetores em R6 dados é(são) paralelo(s) a u= - 2 ,1 ,0 ,3 ,5,1 ?(b) 4 ,- 2 ,0 ,- 6 ,- 10 ,- 2
26 Encontre todos os escalares c1, c2, c3 tais que c 1 1 ,2 ,0 + c 2 2 ,1 ,1 + c 3 0 ,3 ,1 = 0 ,0 ,0
35 Prove as partes (a), (c) e (d) do Teorema 3.1.1.