Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 35
Determine a parte da reta que é visível para um observador situado no ponto , supondo que os planos e sejam opacos.
Passo 1
Beleza, somos observadores no ponto e olhamos pra uma reta. Mas tem dois planos que funcionam ali como muros, nos impedindo de ver a reta inteira. É algo assim olha:
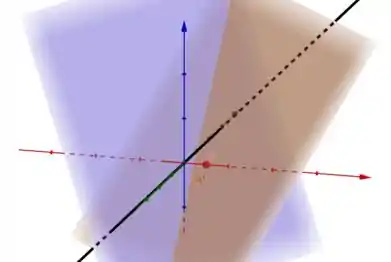
O plano laranja é e o plano roxo é . A reta preta é .
A parte que vemos da reta é a parte que não está tracejada, pois estamos no ponto . De que ponto até que ponto do espaço vai esse trecho da reta que conseguimos ver?
Passo 2
Nós podemos ver a reta a partir do momento que ela passa por até o momento em que ela cruza , concorda? Então, vamos encontrar as intersecções de com e com , pois são as extremidades do segmento que conseguimos ver na reta.
Um ponto genérico da reta é .
Vamos substituir na equação de para encontrarmos sua intersecção com
Substituindo no ponto genérico , encontramos que a intersecção de e é .
Passo 3
Agora vamos substituir o ponto genérico na equação de para encontramos a intersecção de e :
Substituindo no ponto genérico , encontramos que a intersecção de e é .
Então, nós podemos observar a reta no segmento , ou seja, de até ;)
Resposta
Podemos observar a reta no segmento de extremidades e