Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 36

Sejam e Verifique se os planos interceptam o tetraedro .

Passo 1

O plano intercepta os eixos coordenados nos seguintes pontos:

No eixo ( e ):

E esses pontos formam um tetraedro que está fora do tetraedro mencionado no enunciado (o ponto é a origem ok?):

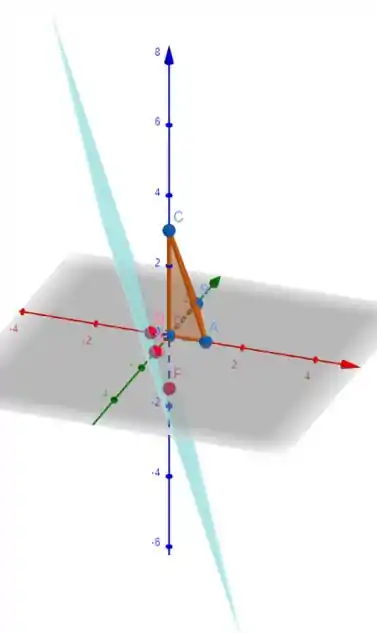
Esses pontos estão em rosa no gráfico acima (pontos D, E e F), e na imagem podemos ver que realmente o plano não corta o tetraedro.

Passo 2

Já encontrando os pontos no qual o plano atravessa os eixos ordenados nós teremos:

E esses pontos estão dentro do tetraedro (o ponto é mais distante da origem que , mais distante que e mais distante da origem que , bastava apenas um desses pontos ser mais distante para o plano atravessar o tetraedro na real.

A imagem acima deve deixar as coisas mais claras.

Resposta

Apenas o plano atravessa o tetraedro.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

32- O vértice de uma pirâmide regular é P = 3 2 , 1 2 , 1 2 e sua base é um quadrado A B C D de centro Q , contido em O x y . Um dos lados do quadrado tem extremidades B = ( 1,0 , 0 ) e C = ( 1,1 , 0

Obtenha uma equação geral do plano que contém a origem O = 0,0 , 0 e forma ângulos de 60° com a reta r : X = 1,1 , 1 + λ 0,1 , - 1 e com o plano π : x - y + 4 = 0 .

Determine o ponto do plano π : 2 x - y + z - 2 = 0 tal que a soma de suas distâncias a P e Q seja a menor possível. P = 2,1 , 0 , Q = 1 , - 1 , - 1 P = 2,1 , 0 , Q = 0,1 , 1 P = 2,1 , 0 , Q = 1 , - 1,

Determine o ponto do plano π : x - 3 y + 2 z = 0 tal que o módulo da diferença entre suas distâncias a P e Q seja o maior possível. P = 3,0 , 2 , Q = 1 , - 1,3 P = 3,0 , 2 , Q = - 1,0 , - 1 P = 3,0 ,