Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 6.Exercício - Ex. 1
Sejam . Prove:
a) e são coplanares é LD.
b) e são colineares é LD.
Passo 1
a) Sejam os pontos e genéricos coplanares:
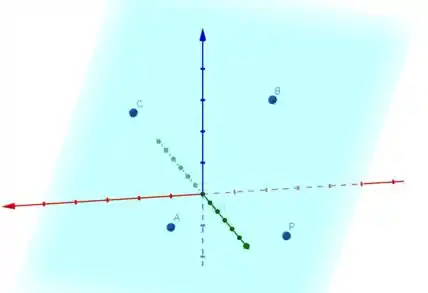
Vamos formar os vetores :
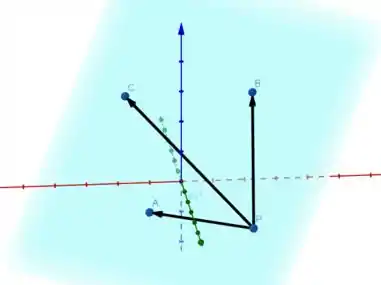
Repare que os 3 vetores são paralelos ao mesmo plano, em azul, logo, são linearmente dependentes :)
Passo 2
b) Se são colineares, teremos que
Disso, temos que e são paralelos certo? E dois vetores paralelos sempre serão LD ;)
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
23. (Requer Cálculo) Em cada parte, use o wronskiano para mostrar que o conjunto de vetores dado é linearmente independente.(a) 1 ,x ,e x (b) 1 ,x ,x 2
21. As funções f 1 x = x e f 2 x = cos x são linearmente independentes em F ( - ∞ , ∞ ) porque nenhuma das duas é um múltiplo escalar da outra. Confirme a independência linear usando o teste do wron
5. Suponha que v 1 → , v 2 → e v 3 → sejam vetores em R 3 com pontos iniciais na origem. Em cada parte, determine se os vetores estão num mesmo plano.(a) v 1 → = 2 ,- 2 ,0 ,v 2 → = 6,1 , 4 ,v 3 → = (
7. (a) Mostre que os três vetores v 1 → = 0 ,3 ,1 ,- 1 ,v 2 → = 6 ,0 ,5 ,1 ,v 3 → = ( 4 ,- 7 ,1 ,3 ) formam um conjunto linearmente dependente em R 4 .(b) Expresse cada vetor da parte (a) como uma com
8. (a) Mostre que os três vetores v 1 → = 1 ,2 ,3 ,4 ,v 2 → = 0 ,1 ,0 , - 1 ,v 3 → = ( 1 ,3 , 3 ,3 ) formam um conjunto linearmente dependente em R 4 .(b) Expresse cada vetor da parte (a) como uma com