Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 20.Exercício - Ex. 37

Um dos diedros determinados pelos planos π 1 : x + 2 y - 2 z - 1 = 0 e π 2 : 2 x + y + 2 z + 2 = 0 contém a origem O = ( 0 ,   0 ,   0 ) . Obtenha uma equação geral do seu plano bissetor.

Passo 1

Para encontrarmos os planos bissetores, basta encontrarmos o lugar geométrico de pontos X = ( x ,   y ,   z ) tais que

d X ,   π 1 = d X ,   π 2

Sabemos que a fórmula de distância entre um ponto B = ( e ,   f ,   g ) e um plano π ' :   a x + b y + c z + d = 0 é

d B ,   π ' = a . e + b . f + c . g + d a 2 + b 2 + c ²

Passo 2

Queremos:

d X ,   π 1 = d X ,   π 2

Sabendo que π 1 : x + 2 y - 2 z - 1 = 0 e π 2 : 2 x + y + 2 z + 2 = 0 , P = ( x ,   y ,   z ) , temos

1 . x + 2 . y - 2 . z - 1 1 2 + 2 2 + ( - 2 ) ² = 2 . x + 1 . y + 2 . z + 2 2 2 + 1 2 + 2 2

x + 2 y - 2 z - 1 9 = 2 x + y + 2 z + 2 9

Como os denominadores são iguais:

x + 2 y - 2 z - 1 = 2 x + y + 2 z + 2

Daí temos dois lugares geométricos, pois estamos lidando com módulos hehe

Vamos calcular primeiro para tudo sem sinal negativo:

x + 2 y - 2 z - 1 = 2 x + y + 2 z + 2

p 1 :   x - y + 4 z + 3 = 0

Agora com sinal negativo:

- ( x + 2 y - 2 z - 1 ) = 2 x + y + 2 z + 2

- x - 2 y + 2 z + 1 = 2 x + y + 2 z + 2

p 2 :   3 x + 3 y + 1 = 0

Passo 3

Beleza, temos dois planos bissetores certo?

Agora queremos saber qual desses planos bissetores está no diedro que contém O = 0 ,   0 ,   0

Se liga, só pra enxergarmos geometricamente, aí embaixo em azul temos os planos do enunciado e em vermelho temos os planos p 1 e p 2 que encontramos

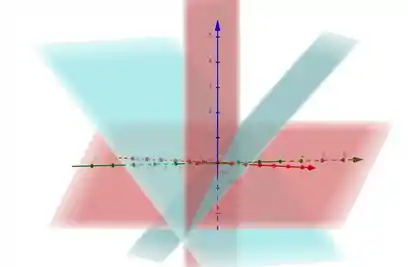
O que vamos fazer é o seguinte: vamos pegar um ponto A qualquer de p 1 e vamos analisar:

Se π 1 separa A e O , ou seja, está entre eles, o plano que queremos é p 2

Se π 1 não separa A e O , o plano que queremos é p 1 mesmo beleza?

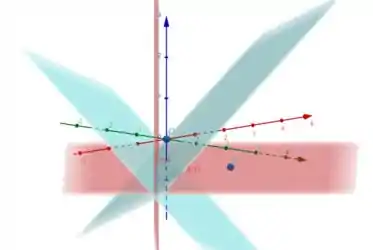
Passo 4

Sabemos que p 1 :   x - y + 4 z + 3 = 0 . Vamos encontrar um ponto A desse plano: se x = 0 e y = 0 , temos que um ponto desse plano bissetor é A = 0 ,   0 ,   - 3 4

Vamos ver se o plano π 1 : x + 2 y - 2 z - 1 = 0 separa A e O . Vamos substituir o vetor O A → = A - O = 0 ,   0 ,   - 3 4 :

0 + 2 . 0 - 2 . - 3 4 - 1

6 4 - 1

2 4 > 0

Como obtivemos um valor maior que 0 , então π 1 separa A e O (da mesma forma que pudemos observar na imagem do passo anterior), portanto, o plano que está no diedro que contém O é o plano p 2 :   3 x + 3 y + 1 = 0 .

Resposta

3 x + 3 y + 1 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escolhendo o sistema de eixos adequado, mostre que, dados dois pontos AeB , o conjunto dos pontos P do espaço tais que d ( P ,A ) ²-d ( P ,B ) ²=c ² ² (uma constante) é um plano perpendicular `a reta
Ache a equação do plano paralelo ao plano 2x − y + 5z − 3 = 0 e que passa por P = (1, −2, 1).
d) Determine a altura do tetraedro relativa a face contida no plano π .
São dados ⎧x= 1 + t⎧ r⎢y= 2- t ⎢ ⎩z= 1 + t⎩ e P=( 2,1 , 0 ) .Dê uma equação do plano π que passa por P e é perpendicular a r .Calcule a interseção do plano π com a reta r .Ache o simétrico de P em rel
Dê equações da reta r que passa pelo ponto P= ( 2 , - 2,3 ) e é perpendicular ao plano π:x- y+ 3 z- 2= 0 .Calcule a interseção de r como plano π .Calcule a distância de P a π .