Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 9.1 - Ex. 7

Encontre a decomposição LU da matriz de coeficientes e, depois, use o método do Exemplo 1 para resolver o sistema.

Passo 1

Vamos lembrar que a fatoração LU possui duas matrizes:

- L: é uma matriz triangular inferior e possui a diagonal principal com o número 1

- U: é uma matriz triangular superior

Tá, mais ainda não conseguiu enxergar? Se lembre o que o triângulo são os números, e não o zero! Vejamos um exemplo:

Lembrando que podem ser quaisquer números!

Maaaas, você reparou que as matrizes estão diferentes da LU?

É isso que o exercício quer! Ele quer como no exemplo e como como a fatoração LU!

Passo 2

Nossa sistema é:

Só que a fim de facilitar as contas, podemos simplificar a primeira linha por 5, e a terceira por 2, lembrando que o resultado também deve ser levado em conta!

A matriz que vamos decompor em LU é

Agora vamos fazer um escalonamento, e percebemos que temos de zerar onde está -8 e 2.

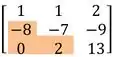
Passo 3

O nosso pivô será o 1 da primeira linha, e temos que zerar com o -8, então vamos pegar seu oposto (8).

Então multiplicaremos a primeira linha pelo valor que encontramos pela segunda linha

Maas quando for passar a matriz, a linha que estamos multiplicando sempre copiamos!

E com 1 como pivô e o oposto de 2

Assim

Temos a matriz U!

Passo 4

Agora, para a gente montar a matriz L, temos que lembrar como ela é:

Assim, entramos em outro sistema de equações:

Logo

Substituímos os valores encontrados:

Passo 5

Vamos fazer o método no qual está escrito no exemplo do exercício, começando com o escalonamento. A diferença que normalmente fazemos e escalonamento por “baixo”, dessa vez faremos por “cima”, e o multiplicador será: