Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 9.5 - Ex. 9
Encontre uma decomposição em valores singulares de A.
Passo 1
Primeiro temos de encontrar os autovalores de , para podermos encontrar os valores singulares de .
Agora calculando o determinante da nossa matriz pela matriz identidade
Assim temos que:
Passo 2
Agora temos de encontrar os autovetores unitários não-nulos correspondentes aos nossos autovalores.
Assim:
Assim:
Finalmente podemos achar nossos vetores colunares da nossa matriz ortogonal .
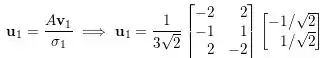
Passo 3
Assim nossa decomposição de valores singulares fica:
Resposta
Exercícios de Livros Relacionados
Nos exercícios 15-16, use a decomposição P L U dada de A para resolver o sistema A x = b reescrevendo-o como P - 1 A x = P - 1 b e resolvendo esse sistema por decomposição L U . b = 215; A =014122311
Nos exercícios 17-18, use a decomposição P L U dada de A para resolver o sistema A x = b , usando o método dos Exercícios 15 e 16. A =3 - 1 0 3 - 1 1 0 2 1 ; b = - 2 1 4
Nos Exercícios 1-2, são dados os autovalores distintos de uma matriz A . Em cada caso, determine se A tem um autovalor dominante e, se tiver, encontre-o. aλ 1 = 7 ,λ 2 = 3 ,λ 3 = - 8 ,λ 4 = 1 bλ 1 = -
Nos Exercícios 1-2, são dados os autovalores distintos de uma matriz A . Em cada caso, determine se A tem um autovalor dominante e, se tiver, encontre-o. aλ 1 = 1 ,λ 2 = 0 ,λ 3 = - 3 ,λ 4 = 2 bλ 1 = -
Sejam V e W espaços vetoriais, T, T1 e T2 transformações lineares de V em W e k um escalar. Defina novas transformações T 1 + T 2 e k T pelas fórmulas T 1 + T 2 x = T 1 x + T 2 ( x ) k T x = k ( T x )