Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.5 - Ex. 8
Encontre a equação da parábola com vértice em e diretriz .
Passo 1
Se liga! A equação de uma parábola com diretriz vertical é:
Esse valor é igualzinho à distância do vértice até a diretriz! Então vamos calcular?
Passo 2
A distância de um ponto até uma reta vertical é só a diferença entre as coordenadas horizontais deles, faz sentido? Tipo assim:
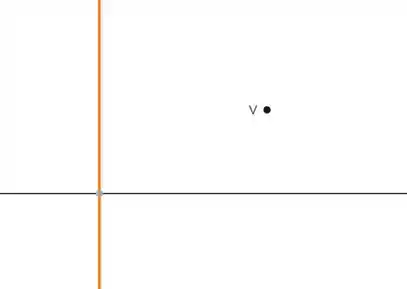
Então beleza, a distância entre o ponto e a reta é:
Passo 3
Então fechou, já temos as coordenadas do vértice e o valor do , daí vamos escrever a equação da parábola!
Resposta
Exercícios de Livros Relacionados
Encontre a equação da elipse com centro em ( 1 ,- 1 ) , semi eixo maior 6 , excentricidade e = 2 3 e semi eixo maior vertical.
Encontre a equação da elipse com focos em ( - 1 ,0 ) e ( 5 ,0 ) e semi eixo maior 2 3 .
Encontre a equação da elipse com centro em ( 1 ,- 1 ) , semi eixo maior 6 , excentricidade e = 2 3 e semi eixo maior vertical.
Encontre a equação da elipse com focos em ( 0 ,0 ) e ( 0 ,10 ) , e semi eixo maior 5 5 .