Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.1 - Ex. 22
Encontre um produto interno euclidiano ponderado em no qual o círculo unitário seja a elipse mostrada na figura dada.
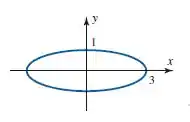
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos a elipse da forma:
Com e .
Portanto:
Passo 2
Sabendo isso, temos que:
Logo:
Logo:
Assim, podemos dizer que é o produto interno ponderado produzido pela norma especificada.
Os pesos do produto interno são:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam U = u 1 u 3u 2 u 4 e V = u 1 u 3u 2 u 4 . Mostre que U , V = u 1 v 1 + u 2 v 3 + u 3 v 2 + u 4 v 4 não define um produto interno em M 22 .
Sejam u , v o produto interno euclidiano em R 2 gerado por 2 11 1 e u = 2,1 , v = - 1,1 , w = 0 , - 1 . Calcule as expressões dadas. u , v v , w u + v , w v d v , w v - w 2
Use a Fórmula 4 para mostrar que u , v = 5 u 1 v 1 - u 1 v 2 - u 2 v 1 + 10 u 2 v 2 é o produto interno em R 2 gerado por A = 2 - 11 3 Use o produto interno da parte a para calcular u , v com u = 0 ,
Repita o E x e r c í c i o1 í com o produto interno euclidiano ponderado u , v = 2 u 1 v 1 + 3 u 2 v 2 .