Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 12.Problemas - Ex. 12

Esboce o conjunto dos pontos do plano cujas coordenadas satisfazem a equação

x³ + xy² − x – x²y – y³ + y = 0.

Passo 1

Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??

Vamos começar manipulando a equação colocando termos em comum em evidência.

x 3 + x y 2 - x - x 2 y - y 3 + y = 0

x ( x 2 + y 2 - 1 ) - y ( x 2 + y 2 - 1 ) = 0

( x - y ) ( x 2 + y 2 - 1 ) = 0

Para que esse produto seja igual à zero um de seus fatores precisa ser zero, assim, temos que:

x - y = 0         o u       x 2 + y 2 - 1 = 0

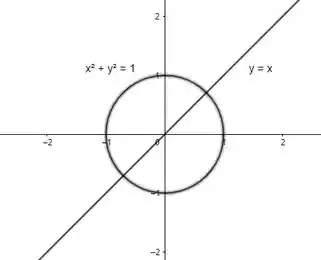
Da primeira equação temos a reta y = x que é a bissetriz do primeiro e terceiro quadrante.

Da segunda equação temos a circunferência x 2 + y 2 = 1 de centro na origem e raio 1.

Esboçando as duas equações num mesmo gráfico, temos o seguinte conjunto de pontos que satisfazem a equação inicial:

Resposta

Confira o esboço feito acima.

Exercícios de Livros Relacionados

Sejam A = 0 ,2 ,1 e r : X = 0 ,2 ,- 2 + λ ( 1 ,- 1 ,2 ) . Obtenha os pontos de r que distam 3 de A . Em seguida verifique se a distância do ponto A à reta r é maior, menor ou igual a 3 e justifique su
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:b) A = - 2 ,3 ,4 ,B = ( - 6 ,- 1 ,6 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:d) A = 1 ,2 ,7 ,B = ( - 5 ,- 4 ,- 5 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:c) A = - 1 ,1 ,2 ,B = ( - 5 ,- 3 ,4 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:a) A = 0 ,3 ,0 ,B = ( 6 ,3 ,3 )