Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 18a
Sejam e . Determine um ponto da reta tal que a área do triângulo seja , nos casos:
a)
Passo 1
Antes de qualquer coisa, vamos encontrar a reta ta bom?
Essa reta passa por e por e tem vetor diretor :
Então, a equação vetorial da reta vai ser:
Olha, a gente escolheu pra ser o ponto da equação, mas você poderia colocar também ta bom?
Passo 2
Agora a gente vai pegar um ponto genérico da reta , a partir da equação dela (lembra que se você tiver colocado o ponto como o ponto na equação, esse ponto genérico vai ser diferente, mas o resultado final é igual fechou?)
Belezinha, agora a partir desse ponto genérico a gente vai fazer nossos cálculos da área do triângulo :D
Passo 3
Queremos que a área do triângulo seja 9 né? A gente sabe que a área do triângulo é metade do módulo do produto vetorial entre e , então vamos encontrar esses vetores:
Fazendo o produto vetorial :
Agora vamos encontrar o módulo desse produto vetorial:
Abrindo os quadrados:
Passo 4
Agora, por último, queremos que :
Elevando os dois lados ao quadrado:
Dividindo tudo por 36:
Resolvendo essa equação do 2° grau, encontramos
Então, os pontos que formam um triângulo de área 9 com e são:
Então, na figura abaixo, tanto o triângulo verde como o azul têm área 9 :)
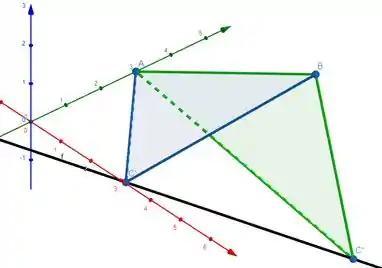
Resposta
a)