Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 15
Sejam e . Obtenha os pontos de que distam de . Em seguida verifique se a distância do ponto à reta é maior, menor ou igual a e justifique sua resposta.
Passo 1
Primeiro vamos escrever um ponto genérico de a partir da sua equação:
Para que o ponto de diste de , vamos usar a fórmula da distância entre pontos e igualar a , ó:
Elevando os dois lados ao quadrado:
Bora abrir esse produto notável aí hahaha
Resolvendo essa equação do segundo grau, encontramos apenas uma raíz: . Isso quer dizer que só existe um que tem a distância até sacou?
Passo 2
Cara, a distância entre o ponto e a reta é exatamente e pra vermos isso não precisamos nem fazer conta porque olha só: só encontramos um ponto de cuja distância dele até é . Isso quer dizer que essa distância foi medida perpendicularmente à reta , se encontrássemos dois pontos, cada um estaria pra um lado de . Se essa distância foi medida perpendicularmente, ela foi medida igualzinho a gente mede a distância de um ponto até uma reta, entãoo, a distância que estávamos usando é a mesma distância entre eles.
Olha uma imagem pra entender melhor:
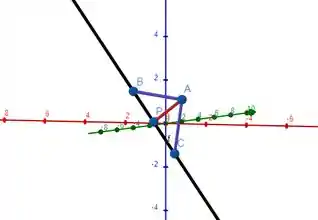
Se encontrássemos dois pontos diferentes para (representados por e na imagem) não teríamos segmentos perpendiculares e com certeza o exercício teria pedido pontos que distem um valor diferente de , mas só encontramos um, que é exatamente a projeção do ponto na reta .
Resposta
Igual a