Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 18c
Sejam e . Determine um ponto da reta tal que a área do triângulo seja , nos casos:
c)
Passo 1
Antes de qualquer coisa, vamos encontrar a reta ta bom?
Essa reta passa por e por e tem vetor diretor :
Então, a equação vetorial da reta vai ser:
Olha, a gente escolheu pra ser o ponto da equação, mas você poderia colocar também ta bom?
Passo 2
Agora a gente vai pegar um ponto genérico da reta , a partir da equação dela (lembra que se você tiver colocado o ponto como o ponto na equação, esse ponto genérico vai ser diferente, mas o resultado final é igual fechou?)
Belezinha, agora a partir desse ponto genérico a gente vai fazer nossos cálculos da área do triângulo :D
Passo 3
Queremos que a área do triângulo seja 9 né? A gente sabe que a área do triângulo é metade do módulo do produto vetorial entre e , então vamos encontrar esses vetores:
Fazendo o produto vetorial :
Opa, de novo o produto vetorial sumiu com nosso :/ mas de qualquer forma vamos fazer as contas pra ver se a área do triângulo vai dar 9:
Passo 4
Calculando a área do triângulo
Eitaaa! Mesmo a gente não achando um valor específico de pra área ser 9, a área acabou sendo 9 de qualquer jeito hahaha
Isso quer dizer que pra qualquer ponto da reta , a área do triângulo vai ser 9 :P
Aí na figura termos exemplos de triângulos formados com e pontos quaisquer da reta , eles sempre vão ter área 9 por pura geometria :D
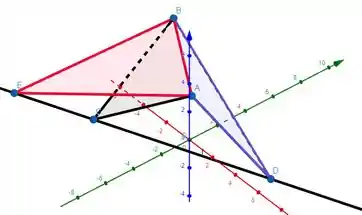
Resposta
c) Para todo ponto de , as condições são satisfeitas :D