Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1e
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
Temos um termo negativo em , o que quer dizer que temos uma hipérbole! Essa hipérbole não toca o eixo . Na forma canônica:
Temos uma elipse com .
Passo 2
Fazendo um esboço, temos:
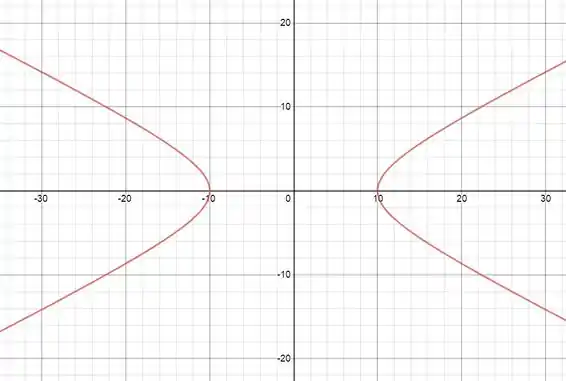
Passo 3
Os focos da nossa hipérbole estão em , onde:
Quanto à sua excentricidade:
E suas diretrizes:
Resposta
Exercícios de Livros Relacionados
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 4 y 2 - x 2 = 16
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. x 2 - y 2 + 8 x - 2 y - 21 = 0
Identificar a cônica, achar a equação no último sistema de coordenadas. 3 x 2 - 8 x y - 12 y 2 + 81 = 0 ;
Identificar a cônica, achar a equação no último sistema de coordenadas. 5 x 2 + 12 x y - 12 13 x = 36 ;
Identificar a cônica, achar a equação no último sistema de coordenadas. 2 x 2 - 4 x y - y 2 = - 24 ;