Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1c

Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.

x 2 25 + y 2 9 = 1

Passo 1

Como ambos os termos quadráticos são positivos, temos uma cônica! Ela já está praticamente na forma canônica, só falta colocarmos os termos nos denominadores em termos quadrados:

x 2 5 2 + y 2 3 2 = 1

Agora sim! Temos a = 5 e b = 3 , a nossa parábola está com seu eixo maior no eixo x indo de - 5 a 5 e seu eixo menor indo de - 3 a 3 no eixo y .

Passo 2

O gráfico dela fica assim:

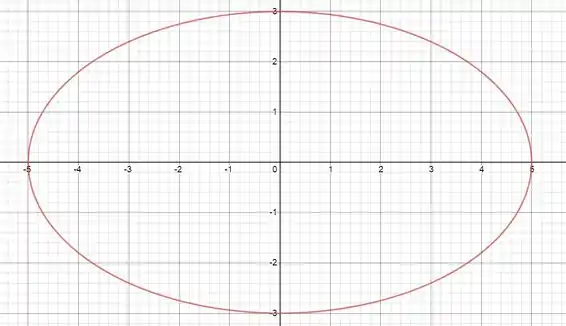
Passo 3

Da definição temos seus focos em F 1 = - c ,   0 e F 2 = c ,   0 . Onde c = a 2 - b 2

c = 25 - 9 = 4

Sua excentricidade é dada por:

e = c a = 4 5

E a suas retas diretrizes:

x = - a e ; x = a e

→ x = ± 5 4 5 = ± 25 4

Resposta

F 1 = - 4 ,   0 ;   F 2 = 4 ,   0

x = ± 25 4

e = 4 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Vértices em ( - 2,0 ) e ( 2 ,0 ) e um eixo conjugado com comprimento 6.
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Centro na origem, focos sobre o eixoy e passando pelos pontos ( - 2 ,4 ) e ( - 6 ,7 ) .
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Centro em 3 ,- 5 , um vértice em 7 ,- 5 e um foco 8 ,- 5 .
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Extremidade do eixo conjugado em ( 0 ,- 3 ) e 0 ,3 e um foco em 5 ,0 .
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Um foco em 26 ,0 e como assíntotas as retas 12 y = ±5 x .